Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T06:45:23.918Z Has data issue: false hasContentIssue false
  • English
  • Français

On the surface expression of bottom features in free-surface flow

Published online by Cambridge University Press:  13 August 2020

Saksham Gakhar Open the ORCID record for Saksham Gakhar [Opens in a new window] ,
Jeffrey R. Koseff Open the ORCID record for Jeffrey R. Koseff [Opens in a new window]  and
Nicholas T. Ouellette Open the ORCID record for Nicholas T. Ouellette [Opens in a new window]
Saksham Gakhar*
Affiliation:
Department of Civil and Environmental Engineering, The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Stanford University, Stanford, CA94305, USA
Jeffrey R. Koseff
Affiliation:
Department of Civil and Environmental Engineering, The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Stanford University, Stanford, CA94305, USA
Nicholas T. Ouellette
Affiliation:
Department of Civil and Environmental Engineering, The Bob and Norma Street Environmental Fluid Mechanics Laboratory, Stanford University, Stanford, CA94305, USA
*
†Email address for correspondence: sakshamg@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

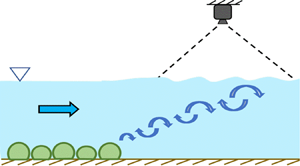
Laboratory experiments were carried out in an open-channel recirculating water flume for different bottom treatments and a variety of flow conditions. We acquired overhead images of the free surface downstream of the bottom features and used these to train convolutional neural network based classifiers. Using these classifiers, we demonstrate that information acquired at the surface alone can be used to differentiate between the physical features that lie at the bottom boundary. We show that although external physical processes, such as winds, can modulate the free surface, they do not necessarily eliminate the free-surface signature of the submerged bottom features. Our results provide strong motivation for future studies that probe the physical processes responsible for transporting information about the bottom of the flow to the surface.

JFM classification

Geophysical and Geological Flows: Topographic effects Waves/Free-surface Flows: Channel flow Geophysical and Geological Flows: Shallow water flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 900 , 10 October 2020 , A41
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abadi, M., Barham, P., Chen, J., Chen, Z., Davis, A., Dean, J., Devin, M., Ghemawat, S., Irving, G., Isard, M., et al. 2016 Tensorflow: a system for large-scale machine learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, pp. 265–283. USENIX Association.Google Scholar
Barsic, P. H. & Chinn, C. R. 2012 Sea surface slope recovery through passive polarimetric imaging. In 2012 Oceans. IEEE.CrossRefGoogle Scholar
Brocchini, M. & Peregrine, D. H. 2001 The dynamics of strong turbulence at free surfaces. Part 1. Description. J. Fluid Mech. 449, 225–254.CrossRefGoogle Scholar
Chickadel, C. C., Horner-Devine, A. R., Talke, S. A. & Jessup, A. T. 2009 Vertical boil propagation from a submerged estuarine sill. Geophys. Res. Lett. 36 (10), L10601.CrossRefGoogle Scholar
Chollet, F., et al. 2015 Keras. https://keras.io.Google Scholar
Cobelli, P. J., Petitjeans, P., Maurel, A. & Pagneux, V. 2018 Determination of the bottom deformation from space- and time-resolved water wave measurements. J. Fluid Mech. 835, 301–326.CrossRefGoogle Scholar
Dabiri, D. & Gharib, M. 2001 Simultaneous free-surface deformation and near-surface velocity measurements. Exp. Fluids 30 (4), 381–390.CrossRefGoogle Scholar
Holman, R. & Haller, M. C. 2013 Remote sensing of the nearshore. Annu. Rev. Marine Sci. 5 (1), 95–113.CrossRefGoogle ScholarPubMed
Koltakov, S. 2013 Bathymetry inference from free-surface flow features using large-eddy simulation. PhD thesis, Stanford University.Google Scholar
Kumar, S., Gupta, R. & Banerjee, S. 1998 An experimental investigation of the characteristics of free-surface turbulence in channel flow. Phys. Fluids 10 (2), 437–456.CrossRefGoogle Scholar
Logory, L. M., Hirsa, A. & Anthony, D. G. 1996 Interaction of wake turbulence with a free surface. Phys. Fluids 8 (3), 805–815.CrossRefGoogle Scholar
Mandel, T. 2018 Free-surface dynamics in the presence of submerged canopies. PhD thesis, Stanford University.Google Scholar
Mandel, T. L., Gakhar, S., Chung, H., Rosenzweig, I. & Koseff, J. R. 2019 On the surface expression of a canopy-generated shear instability. J. Fluid Mech. 867, 633–660.CrossRefGoogle Scholar
Mandel, T. L., Rosenzweig, I., Chung, H., Ouellette, N. T. & Koseff, J. R. 2017 Characterizing free-surface expressions of flow instabilities by tracking submerged features. Exp. Fluids 58 (11), 153.CrossRefGoogle Scholar
Narayanan, C., Rama Rao, V. N. & Kaihatu, J. M. 2004 Model parameterization and experimental design issues in nearshore bathymetry inversion. J. Geophys. Res. 109 (C8), C08006.CrossRefGoogle Scholar
Nazarenko, S. & Lukaschuk, S. 2016 Wave turbulence on water surface. Annu. Rev. Condens. Matter Phys. 7 (1), 61–88.CrossRefGoogle Scholar
Nepf, H. M. & Vivoni, E. R. 2000 Flow structure in depth-limited, vegetated flow. J. Geophys. Res. 105 (C12), C900145.CrossRefGoogle Scholar
O'Riordan, C. A., Monismith, S. G. & Koseff, J. R. 1993 A study of concentration boundary-layer formation over a bed of model bivalves. Limnol. Oceanogr. 38 (8), 1712–1729.CrossRefGoogle Scholar
Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., Blondel, M., Prettenhofer, P., Weiss, R., Dubourg, V., et al. 2011 Scikit-learn: machine learning in Python. J. Machine Learning Res. 12, 2825–2830.Google Scholar
Plant, W. J., Branch, R., Chatham, G., Chickadel, C. C., Hayes, K., Hayworth, B., Horner-Devine, A., Jessup, A., Fong, D. A., Fringer, O. B., et al. 2009 Remotely sensed river surface features compared with modeling and in situ measurements. J. Geophys. Res. 114 (C11), C11002.CrossRefGoogle Scholar
Reidenbach, M. A., Koseff, J. R., Monismith, S. G., Steinbuckc, J. V. & Genin, A. 2006 The effects of waves and morphology on mass transfer within branched reef corals. Limnol. Oceanogr. 51 (2), 1134–1141.CrossRefGoogle Scholar
Rosenzweig, I. 2017 Experimental investigation of the surface expression of a canopy-induced shear instability. PhD thesis, Stanford University.Google Scholar
Savelsberg, R. & van de Water, W. 2008 Turbulence of a free surface. Phys. Rev. Lett. 100, 034501.CrossRefGoogle ScholarPubMed
Sokoray-Varga, B. & Józsa, J. 2008 Particle tracking velocimetry (PTV) and its application to analyse free surface flows in laboratory scale models. Periodica Polytechnica Civ. Engng 52 (2), 63–71.CrossRefGoogle Scholar
Stone, M. L., Rasmussen, T. J., Bennett, T. J., Poulton, B. C. & Ziegler, A. C. 2012 Protocols for collection of streamflow, water-quality, streambed-sediment, periphyton, macroinvertebrate, fish, and habitat data to describe stream quality for the hydrobiological monitoring program, Equus beds aquifer storage and recovery program, city of Wichita, Kansas. p. 7.CrossRefGoogle Scholar
Takeda, M., Ina, H. & Kobayashi, S. 1982 Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 72 (1), 156–160.CrossRefGoogle Scholar
Takeda, M. & Mutoh, K. 1983 Fourier transform profilometry for the automatic measurement of 3-D object shapes. Appl. Opt. 22 (24), 3977–3982.CrossRefGoogle ScholarPubMed
Wilson, G. & Özkan Haller, H. T. 2012 Ensemble-based data assimilation for estimation of river depths. J. Atmos. Ocean. Technol. 29 (10), 1558–1568.CrossRefGoogle Scholar
Zappa, C. J., Banner, M. L., Schultz, H., Corrada-Emmanuel, A., Wolff, L. B. & Yalcin, J. 2008 Retrieval of short ocean wave slope using polarimetric imaging. Meas. Sci. Technol. 19 (5), 055503.CrossRefGoogle Scholar