Article contents
The onset of strongly localized thermal convection in rotating spherical shells
Published online by Cambridge University Press: 16 November 2011
Abstract
A Boussinesq fluid of kinematic velocity  and thermal diffusivity
and thermal diffusivity  is confined within a rapidly rotating shell with inner and outer sphere boundary radii
is confined within a rapidly rotating shell with inner and outer sphere boundary radii 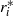 and
and 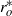 , respectively. The boundaries of the shell corotate at angular velocity
, respectively. The boundaries of the shell corotate at angular velocity 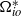 and a continuously varying stratification profile is applied which is unstable in
and a continuously varying stratification profile is applied which is unstable in 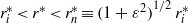 and stable in
and stable in 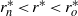 . When
. When 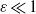 , the unstable zone attached to the inner boundary is thin. As in previous small Ekman number
, the unstable zone attached to the inner boundary is thin. As in previous small Ekman number 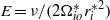 studies, convection at the onset of instability takes on the familiar ‘cartridge belt’ structure, which is localized within a narrow layer adjacent to, but outside, the cylinder tangent to the inner sphere at its equator (Dormy et al. J. Fluid Mech., 2004, vol. 501, pp. 43–70), with estimated radial width of order
studies, convection at the onset of instability takes on the familiar ‘cartridge belt’ structure, which is localized within a narrow layer adjacent to, but outside, the cylinder tangent to the inner sphere at its equator (Dormy et al. J. Fluid Mech., 2004, vol. 501, pp. 43–70), with estimated radial width of order 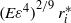 . The azimuthally propagating convective columns, described by the cartridge belt, reside entirely within the unstable layer when
. The azimuthally propagating convective columns, described by the cartridge belt, reside entirely within the unstable layer when  , and extend from the equatorial plane an axial distance
, and extend from the equatorial plane an axial distance 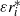 along the tangent cylinder as far as its intersection with the neutrally stable spherical surface
along the tangent cylinder as far as its intersection with the neutrally stable spherical surface 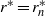 . We investigate the eigensolutions of the ordinary differential equation governing the axial structure of the cartridge belt both numerically for moderate-to-small values of the stratification parameter
. We investigate the eigensolutions of the ordinary differential equation governing the axial structure of the cartridge belt both numerically for moderate-to-small values of the stratification parameter  and analytically when
and analytically when 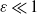 . At the lowest order of the expansion in powers of
. At the lowest order of the expansion in powers of  , the eigenmodes resemble those for classical plane layer convection, being either steady (exchange of stabilities) or, for small Prandtl number
, the eigenmodes resemble those for classical plane layer convection, being either steady (exchange of stabilities) or, for small Prandtl number 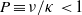 , oscillatory (overstability) with a frequency
, oscillatory (overstability) with a frequency 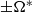 . At the next order, the axial variation of the basic state removes any plane layer degeneracies. First, the exchange of stabilities modes oscillate at a low frequency causing the short axial columns to propagate as a wave with a small angular velocity, termed slow modes. Second, the magnitudes of both the Rayleigh number and frequency of the two overstable modes, termed fast modes, split. When
. At the next order, the axial variation of the basic state removes any plane layer degeneracies. First, the exchange of stabilities modes oscillate at a low frequency causing the short axial columns to propagate as a wave with a small angular velocity, termed slow modes. Second, the magnitudes of both the Rayleigh number and frequency of the two overstable modes, termed fast modes, split. When 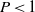 the slow modes that exist at large azimuthal wavenumbers
the slow modes that exist at large azimuthal wavenumbers 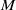 make a continuous transition to the preferred fast modes at small
make a continuous transition to the preferred fast modes at small 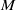 . At all values of
. At all values of 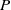 the critical Rayleigh number corresponds to a mode exhibiting prograde propagation, whether it be a fast or slow mode. This feature is shared by the uniform classical convective shell models, as well as Busse’s celebrated annulus model. None of them possess any stable stratification and typically are prone to easily excitable Rossby or inertial modes of convection at small
the critical Rayleigh number corresponds to a mode exhibiting prograde propagation, whether it be a fast or slow mode. This feature is shared by the uniform classical convective shell models, as well as Busse’s celebrated annulus model. None of them possess any stable stratification and typically are prone to easily excitable Rossby or inertial modes of convection at small 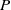 . By way of contrast these structures cannot exist in our model for small
. By way of contrast these structures cannot exist in our model for small  due to the viscous damping in the outer thick stable region.
due to the viscous damping in the outer thick stable region.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2011
References
- 12
- Cited by

