Published online by Cambridge University Press: 07 August 2020
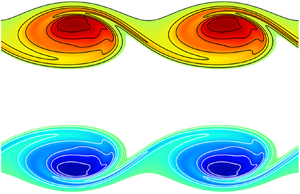
We investigate the development of three-dimensional instabilities on a time-dependent round jet undergoing the axisymmetric Kelvin–Helmholtz (KH) instability. A non-modal linear stability analysis of the resulting unsteady roll-up into a vortex ring is performed based on a direct-adjoint approach. Varying the azimuthal wavenumber  $m$, the Reynolds number
$m$, the Reynolds number  ${Re}$ and the aspect ratio
${Re}$ and the aspect ratio  $\alpha$ of the jet base flow, we explore the potential for secondary energy growth beyond the initial phase when the base flow is still quasi-parallel and universal shear-induced transient growth occurs. For
$\alpha$ of the jet base flow, we explore the potential for secondary energy growth beyond the initial phase when the base flow is still quasi-parallel and universal shear-induced transient growth occurs. For  ${Re}=1000$ and
${Re}=1000$ and  $\alpha = 10$, the helical
$\alpha = 10$, the helical  $m=1$ and double-helix
$m=1$ and double-helix  $m=2$ perturbations stand as global optimals with larger growth rates in the post roll-up phase. The secondary energy growth stems from the development of elliptical (E-type) and hyperbolic (H-type) instabilities. For
$m=2$ perturbations stand as global optimals with larger growth rates in the post roll-up phase. The secondary energy growth stems from the development of elliptical (E-type) and hyperbolic (H-type) instabilities. For  $m>2$, the maximum of the kinetic energy of the optimal perturbation moves from the large scale vortex core towards the thin vorticity braid. With a Reynolds number one order of magnitude larger, the kinetic energy of the optimal perturbations exhibits sustained growth well after the saturation time of the base flow KH wave and the underlying length scale selection favours higher azimuthal wavenumbers associated with H-type instability in the less diffused vorticity braid. Doubling the jet aspect ratio yields initially thinner shear layers only slightly affected by axisymmetry. The resulting unsteady base flow loses scale selectivity and is prone to a common path of initial transient growth followed by the optimal secondary growth of a wide range of wavenumbers. Increasing both the aspect ratio and the Reynolds number thus yields an even larger secondary growth and a lower wavenumber selectivity. At a lower aspect ratio of
$m>2$, the maximum of the kinetic energy of the optimal perturbation moves from the large scale vortex core towards the thin vorticity braid. With a Reynolds number one order of magnitude larger, the kinetic energy of the optimal perturbations exhibits sustained growth well after the saturation time of the base flow KH wave and the underlying length scale selection favours higher azimuthal wavenumbers associated with H-type instability in the less diffused vorticity braid. Doubling the jet aspect ratio yields initially thinner shear layers only slightly affected by axisymmetry. The resulting unsteady base flow loses scale selectivity and is prone to a common path of initial transient growth followed by the optimal secondary growth of a wide range of wavenumbers. Increasing both the aspect ratio and the Reynolds number thus yields an even larger secondary growth and a lower wavenumber selectivity. At a lower aspect ratio of  $\alpha =5$, the base flow is smooth and a genuine round jet affected by the axisymmetry condition. The axisymmetric modal perturbation of the base flow parallel jet only weakly affects the first common phase of transient growth and the optimal helical perturbation
$\alpha =5$, the base flow is smooth and a genuine round jet affected by the axisymmetry condition. The axisymmetric modal perturbation of the base flow parallel jet only weakly affects the first common phase of transient growth and the optimal helical perturbation  $m=1$ dominates with energy gains considerably larger than those of larger azimuthal wavenumbers whatever the horizon time.
$m=1$ dominates with energy gains considerably larger than those of larger azimuthal wavenumbers whatever the horizon time.