Article contents
Oscillations of the large-scale circulation in experimental liquid metal convection at aspect ratios 1.4–3
Published online by Cambridge University Press: 06 October 2022
Abstract
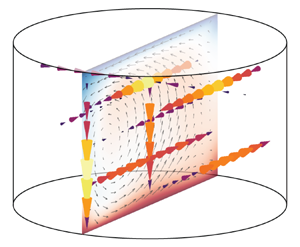
We investigate the scaling properties of the primary flow modes and their sensitivity to aspect ratio in a liquid gallium (Prandtl number  $Pr = 0.02$) convection system through combined laboratory experiments and numerical simulations. We survey cylindrical aspect ratios
$Pr = 0.02$) convection system through combined laboratory experiments and numerical simulations. We survey cylindrical aspect ratios  $1.4 \le \varGamma \le 3$ and Rayleigh numbers
$1.4 \le \varGamma \le 3$ and Rayleigh numbers  $10^{4} \lesssim Ra \lesssim 10^{6}$. In this range the flow is dominated by a large-scale circulation (LSC) subject to low-frequency oscillations. In line with previous studies, we show robust scaling of the Reynolds number
$10^{4} \lesssim Ra \lesssim 10^{6}$. In this range the flow is dominated by a large-scale circulation (LSC) subject to low-frequency oscillations. In line with previous studies, we show robust scaling of the Reynolds number  $Re$ with
$Re$ with  $Ra$ and we confirm that the LSC flow is dominated by a jump-rope vortex (JRV) mode whose signature frequency is present in velocity and temperature measurements. We further show that both
$Ra$ and we confirm that the LSC flow is dominated by a jump-rope vortex (JRV) mode whose signature frequency is present in velocity and temperature measurements. We further show that both  $Re$ and JRV frequency scaling trends are relatively insensitive to container geometry. The temperature and velocity spectra consistently show peaks at the JRV frequency, its harmonic and a secondary mode. The relative strength of these peaks changes and the presence of the secondary peak depend highly on aspect ratio, indicating that, despite having a minimal effect on typical velocities and frequencies, the aspect ratio has a significant effect on the underlying dynamics. Applying a bandpass filter at the secondary frequency to velocity measurements reveals that a clockwise twist in the upper half of the fluid layer coincides with a counterclockwise twist in the bottom half, indicating a torsional mode. For aspect ratio
$Re$ and JRV frequency scaling trends are relatively insensitive to container geometry. The temperature and velocity spectra consistently show peaks at the JRV frequency, its harmonic and a secondary mode. The relative strength of these peaks changes and the presence of the secondary peak depend highly on aspect ratio, indicating that, despite having a minimal effect on typical velocities and frequencies, the aspect ratio has a significant effect on the underlying dynamics. Applying a bandpass filter at the secondary frequency to velocity measurements reveals that a clockwise twist in the upper half of the fluid layer coincides with a counterclockwise twist in the bottom half, indicating a torsional mode. For aspect ratio  $\varGamma = 3$, the unified LSC structure breaks down into multiple rolls in both simulation and experiment.
$\varGamma = 3$, the unified LSC structure breaks down into multiple rolls in both simulation and experiment.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by


