Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T23:11:33.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Pseudophase change effects in turbulent channel flow under transcritical temperature conditions

Published online by Cambridge University Press:  17 May 2019

Kukjin Kim ,
Jean-Pierre Hickey Open the ORCID record for Jean-Pierre Hickey [Opens in a new window]  and
Carlo Scalo
Kukjin Kim
Affiliation:
School of Mechanical Engineering, Purdue University, 585 Purdue Mall, West Lafayette, IN 47907-2088, USA
Jean-Pierre Hickey*
Affiliation:
Department of Mechanical and Mechatronics Engineering, University of Waterloo, 200 University Avenue West, Waterloo, ON N2L 3G1, Canada
Carlo Scalo
Affiliation:
School of Mechanical Engineering, Purdue University, 585 Purdue Mall, West Lafayette, IN 47907-2088, USA
*
†Email address for correspondence: jean-pierre.hickey@uwaterloo.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

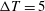We have performed direct numerical simulations of compressible turbulent channel flow using R-134a as a working fluid in transcritical temperature ranges ($\unicode[STIX]{x0394}T=5$, 10 and 20 K, where 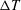$\unicode[STIX]{x0394}T$ is top-to-bottom temperature difference) at supercritical pressure. At these conditions, a pseudophase change occurs at various wall-normal locations within the turbulent channel from 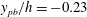$y_{pb}/h=-0.23$ (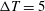$\unicode[STIX]{x0394}T=5$  K) to 0.89 (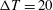$\unicode[STIX]{x0394}T=20$  K), where 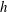$h$ is the channel half-height and $y=0$ the centreplane position. Increase in 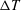$\unicode[STIX]{x0394}T$ also results in increasing wall-normal gradients in the semi-local friction Reynolds number. Classical, compressible scaling laws of the mean velocity profile are unable to fully collapse real fluid effects in this flow. The proximity to the pseudotransitioning layer inhibits turbulent velocity fluctuations, while locally enhancing the temperature and density fluctuation intensities. Probability distribution analysis reveals that the sheet of fluid undergoing pseudophase change is characterized by a dramatic reduction in the kurtosis of density fluctuations, hence becoming thinner as 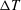$\unicode[STIX]{x0394}T$ is increased. Instantaneous visualizations show dense fluid ejections from the pseudoliquid viscous sublayer, some reaching the channel core, causing positive values of density skewness in the respective buffer layer region (vice versa for the top wall) and an impoverishment of the turbulent flow structure population near pseudotransitioning conditions.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 52 - 91
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Artemenko, S., Krijgsman, P. & Mazur, V. 2017 The Widom line for supercritical fluids. J. Mol. Liq. 238, 122–128.10.1016/j.molliq.2017.03.107Google Scholar
Banuti, D. T. 2015 Crossing the Widom-line – supercritical pseudo-boiling. J. Supercritical Fluids 98, 12–16.Google Scholar
Bradshaw, P. 1994 Turbulence: the chief outstanding difficulty of our subject. Exp. Fluids 16 (3–4), 203–216.Google Scholar
Brazhkin, V. V., Fomin, Y. D., Lyapin, A. G., Ryzhov, V. N. & Tsiok, E. N. 2011 Widom line for the liquid–gas transition in Lennard-Jones system. J. Phys. Chem. B 115 (48), 14112–14115.Google Scholar
Casiano, M. J., Hulka, J. R. & Yang, V. 2010 Liquid-propellant rocket engine throttling: a comprehensive review. J. Propul. Power 26 (5), 897–923.Google Scholar
Chassaing, P., Antonia, R. A., Anselmet, F., Joly, L. & Sarkar, S. 2013 Variable Density Fluid Turbulence, vol. 69. Springer Science & Business Media.Google Scholar
Chung, T.-H., Ajlan, M., Lee, L. L. & Starling, K. E. 1988 Generalized multiparameter correlation for nonpolar and polar fluid transport properties. Ind. Engng Chem. Res. 27 (4), 671–679.10.1021/ie00076a024Google Scholar
Coleman, G. N., Kim, J. & Moser, R. D. 1995 A numerical study of turbulent supersonic isothermal-wall channel flow. J. Fluid Mech. 305, 159–183.Google Scholar
van Driest, E. R. 1951 Turbulent boundary layer in compressible fluids. J. Aero. Sci. 18, 145–160; 216.Google Scholar
Ewing, M. B. & Peters, C. J. 2000 Fundamental Considerations, 1st edn. chap. 2, Elsevier.10.1016/S1874-5644(00)80013-2Google Scholar
Fisher, M. E. & Widom, B. 1969 Decay of correlations in linear systems. J. Chem. Phys. 50 (20), 3756–3772.Google Scholar
Gorelli, F., Santoro, M., Scopigno, T., Krisch, M. & Ruocco, G. 2006 Liquid-like behavior of supercritical fluids. Phys. Rev. Lett. 97 (24), 245702.Google Scholar
Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.Google Scholar
Kawai, S. 2019 Heated transcritical and unheated non-transcritical turbulent boundary layers at supercritical pressures. J. Fluid Mech. 865, 563–601.10.1017/jfm.2019.13Google Scholar
Kawai, S., Terashima, H. & Negishi, H. 2015 A robust and accurate numerical method for transcritical turbulent flows at supercritical pressure with an arbitrary equation of state. J. Comput. Phys. 300 (Suppl. C), 116–135.10.1016/j.jcp.2015.07.047Google Scholar
Kim, K., Hickey, J.-P. & Scalo, C.2017 Numerical investigation of transcritical-T heat-and-mass-transfer dynamics in compressible turbulent channel flow. AIAA Paper 2017-1711.Google Scholar
Kim, K., Scalo, C. & Hickey, J.-P. 2017 Turbulent dynamics and heat transfer in transcritical channel flow. In 10th International Symposium on Turbulence and Shear Flow Phenomena.Google Scholar
Larsson, J., Bermejo-Moreno, I. & Lele, S. K. 2013 Reynolds- and Mach-number effects in canonical shock–turbulence interaction. J. Fluid Mech. 717, 293–321.Google Scholar
Larsson, J. & Lele, S. K. 2009 Direct numerical simulation of canonical shock/turbulence interaction. Phys. Fluids 21, 126101.Google Scholar
Larsson, J., Lele, S. K. & Moin, P. 2007 Effect of numerical dissipation on the predicted spectra for compressible turbulence. In Annual Research Briefs, Center for Turbulence Research.Google Scholar
Lee, J., Jung, S. Y., Sung, H. J. & Zaki, T. A. 2013 Effect of wall heating on turbulent boundary layers with temperature-dependent viscosity. J. Fluid Mech. 726, 196–225.10.1017/jfm.2013.211Google Scholar
Lemmon, E. W., McLinden, M. O. & Friend, D. G. 2016 Thermophysical Properties of Fluid Systems, NIST Chemistry Webbook, NIST Standard Reference Database. National Institute of Standards and Technology.Google Scholar
Liu, L., Chen, S.-H., Faraone, A., Yen, C.-W. & Mou, C.-Y. 2005 Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys. Rev. Lett. 95 (11), 117802.Google Scholar
Ma, P. C., Lv, Y. & Ihme, M. 2017 An entropy-stable hybrid scheme for simulations of transcritical real-fluid flows. J. Comput. Phys. 340 (Suppl. C), 330–357.Google Scholar
Ma, P. C., Yang, X. I. A. & Ihme, M. 2018 Structure of wall-bounded flows at transcritical conditions. Phys. Rev. Fluids 3 (3), 034609.10.1103/PhysRevFluids.3.034609Google Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Min, T. & Kim, J. 2004 Effects of hydrophobic surface on skin-friction drag. Phys. Fluids 16 (7), L55–L58.Google Scholar
Morinishi, Y., Tamano, S. & Nakabayashi, K. 2004 Direct numerical simulation of compressible turbulent channel flow between adiabatic and isothermal walls. J. Fluid Mech. 502, 273–308.Google Scholar
Morkovin, M. V. 1962 Effects of compressibility on turbulent flows. Mécanique de la Turb. 367, 367–380.Google Scholar
Nemati, H., Patel, A., Boersma, B. J. & Pecnik, R. 2015 Mean statistics of a heated turbulent pipe flow at supercritical pressure. Intl J. Heat Mass Transfer 83, 741–752.Google Scholar
Palumbo, M.2009 Predicting the onset of thermoacoustic oscillations in supercritical fluids. Master’s thesis, Purdue University.Google Scholar
Patel, A., Boersma, B. J. & Pecnik, R. 2016 The influence of near-wall density and viscosity gradients on turbulence in channel flows. J. Fluid Mech. 809, 793–820.Google Scholar
Patel, A., Peeters, J. W. R., Boersma, B. J. & Pecnik, R. 2015 Semi-local scaling and turbulence modulation in variable property turbulent channel flows. Phys. Fluids 27, 095101.10.1063/1.4929813Google Scholar
Peeters, J. W. R., Pecnik, R., Rohde, M., van der Hagen, T. H. J. J. & Boersma, B. J. 2016 Turbulence attenuation in simultaneously heated and cooled annular flows at supercritical pressure. J. Fluid Mech. 799, 505–540.Google Scholar
Peng, D.-Y. & Robinson, D. B. 1976 A new two-constant equation of state. Ind. Engng Chem. Fundam. 15 (1), 59–64.10.1021/i160057a011Google Scholar
Pizzarelli, M., Nasuti, F., Paciorri, R. & Onofri, M. 2009 Numerical analysis of three-dimensional flow of supercritical fluid in asymmetrically heated channels. AIAA J. 47, 2534–2543.Google Scholar
Poling, B. E., Prausnitz, J. M. & O’Connell, J. P. 2001 The Properties of Gases and Liquids. McGraw-Hill.Google Scholar
Sciacovelli, L., Cinnella, P. & Gloerfelt, X. 2017 Direct numerical simulations of supersonic turbulent channel flows of dense gases. J. Fluid Mech. 821, 153–199.10.1017/jfm.2017.237Google Scholar
Sciortino, F., Poole, P. H., Essmann, U. & Stanley, H. E. 1997 Line of compressibility maxima in the phase diagram of supercooled water. Phys. Rev. E 55 (1), 727–737.Google Scholar
Sengupta, U., Nemati, H., Boersma, B. J. & Pecnik, R. 2017 Fully compressible low-Mach number simulations of carbon-dioxide at supercritical pressures and trans-critical temperatures. Flow Turbul. Combust. 99, 909–931.Google Scholar
Simeoni, G. G., Bryk, T., Gorelli, F. A., Krisch, M., Ruocco, G., Santoro, M. & Scopigno, T. 2010 The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 6, 503–507.Google Scholar
Terashima, H., Kawai, S. & Yamanishi, N. 2011 High-resolution numerical method for supercritical flows with large density variations. AIAA J. 49, 2658–2672.Google Scholar
Terashima, H. & Koshi, M. 2012 Approach for simulating gas/liquid-like flows under supercritical pressures using a high-order central differencing scheme. J. Comput. Phys. 231 (20), 6907–6923.Google Scholar
Terashima, H. & Koshi, M. 2013 Strategy for simulating supercritical cryogenic jets using high-order schemes. Comput. Fluids 85, 39–46.Google Scholar
The HDF Group 1998 Hierarchical data format, version 5. http://www.hdfgroup.org/HDF5/.Google Scholar
Thurston, R. S.1964 Pressure oscillations induced by forced convection heat transfer to two phase and supercritical hydrogen. Tech. Rep. LAMS-3070. Los Alamos Scientific Laboratory.Google Scholar
Trettel, A. & Larsson, J. 2016 Mean velocity scaling for compressible wall turbulence with heat transfer. Phys. Fluids 28, 026102.Google Scholar
Tucker, S. C. 1999 Solvent density inhomogeneities in supercritical fluids. Chem. Rev. 99, 391–418.Google Scholar
Wang, H., Zhou, J., Pan, Y. & Wang, N. 2015 Experimental investigation on the onset of thermo-acoustic instability of supercritical hydrocarbon fuel flowing in a small-scale channel. Acta Astron. 117, 296–304.10.1016/j.actaastro.2015.08.009Google Scholar
Wen, Q. L. & Gu, H. Y. 2011 Numerical investigation of acceleration effect on heat transfer deterioration phenomenon in supercritical water. Progr. Nucl. Energy 53, 480–486.Google Scholar
Xu, L., Kumar, P., Buldyrev, S. V., Chen, S.-H., Poole, P. H., Sciortino, F. & Stanley, H. E. 2005 Relation between the Widom line and the dynamic crossover in systems with a liquid–liquid phase transition. Proc. Natl Acad. Sci. USA 102 (46), 16558–16562.Google Scholar
Yoo, J. Y. 2013 The turbulent flows of supercritical fluids with heat transfer. Annu. Rev. Fluid Mech. 45, 495–525.Google Scholar
Zhang, L., Liu, M., Dong, Q. & Zhao, S. 2011 Numerical research of heat transfer of supercritical CO2 in channels. Energy Power Engng 3, 167–173.Google Scholar
Zhong, F., Fan, X., Yu, G., Li, J. & Sung, C.-J. 2009 Heat transfer of aviation kerosene at supercritical conditions. J. Thermophys. Heat Transfer 23, 543–550.10.2514/1.41619Google Scholar