Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T19:51:09.716Z Has data issue: false hasContentIssue false
  • English
  • Français

Rapid gravitational adjustment of horizontal shear flows

Published online by Cambridge University Press:  13 March 2013

Brian L. White  and
Karl R. Helfrich
Brian L. White*
Affiliation:
Marine Sciences Department, UNC-Chapel Hill, NC 27599, USA
Karl R. Helfrich
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA 02543, USA
*
†Email address for correspondence: bwhite@unc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The evolution of a horizontal shear layer in the presence of a horizontal density gradient is explored by three-dimensional numerical simulations. These flows exhibit characteristics of both free shear flows and gravity currents, but have complex dynamics due to strong interactions between the turbulent features of each. Vertical vortices produced by horizontal shear are tilted and stretched by the gravitational adjustment, rapidly enhancing vorticity. Shear intensification at frontal convergences produces high-wavenumber vertical vorticity and the slumping of the density interface produces horizontal Kelvin–Helmholtz vortices typical of a gravity current. The interaction between these instabilities promotes a rapid transition to three-dimensional turbulence. 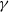The flow development depends on the relative time scales of shear instability and gravitational adjustment, described by a parameter $\gamma $ (where the limits 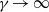$\gamma \rightarrow \infty $ and 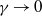$\gamma \rightarrow 0$ represent a pure gravity current and a pure mixing layer, respectively). The growth rate of three-dimensional instability and the mixing increase for smaller 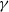$\gamma $. When 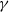$\gamma $ is sufficiently small, there are two distinct regimes: an early period of during which the interface grows rapidly, followed by horizontal diffusive growth. Numerical results are consistent with field observations of tidal separation flows in the Haro Strait (Farmer, Pawlowicz & Jiang, Dyn. Atmos. Oceans., vol. 36, 2002, pp. 43–58), including the magnitude of downwelling vertical currents, horizontal scales of surface vortex features and mixing rate.

JFM classification

Geophysical and Geological Flows: Gravity currents Wakes/Jets: Shear layers Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 86 - 117
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Almgren, A., Bell, J., Colella, P., Howell, L. & Welcome, M. 1998 A conservative adaptive projection method for the variable density incompressible Navier–Stokes equations. J. Comput. Phys. 142, 1–46.Google Scholar
Aspden, A., Nikiforakis, N., Dalziel, S. & Bell, J. B. 2008 Analysis of implicit les methods. Comm. App. Math. Com. Sc. 3 (1), 103–126.Google Scholar
Basak, S. & Sarkar, S. 2006 Dynamics of a stratified shear layer with horizontal shear. J. Fluid Mech. 568, 19–54.Google Scholar
Benjamin, T. 1968 Gravity currents and related phenomena. J. Fluid Mech. 31, 209–248.Google Scholar
Boccaletti, G., Ferrari, R. & Fox-Kemper, B. 2007 Mixed layer instabilities and restratification. J. Phys. Oceanogr. 37 (9), 2228–2250.Google Scholar
Boulanger, N., Meunier, P. & Dizès, S. L. 2008 Tilt-induced instability of a stratified vortex. J. Fluid Mech. 596, 1–20.Google Scholar
Brown, G. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.Google Scholar
Carpenter, J. R., Balmforth, N. J. & Lawrence, G. A. 2010 Identifying unstable modes in stratified shear layers. Phys. Fluids 22 (5), 054104.Google Scholar
Corcos, G. & Lin, S. 1984 The mixing layer - deterministic models of a turbulent-flow 2. The origin of the 3-dimensional motion. J. Fluid Mech. 139 (FEB), 67–95.Google Scholar
Farmer, D., Pawlowicz, R. & Jiang, R. 2002 Tilting separation flows: a mechanism for intense vertical mixing in the coastal ocean. Dyn. Atmos. Oceans. 36 (1–3), 43–58.Google Scholar
Hartel, C., Carlsson, F. & Thunblom, M. 2000a Analysis and direct numerical simulation of the flow at a gravity-current head. Part 2. the lobe-and-cleft instability. J. Fluid Mech. 418, 213–229.Google Scholar
Hartel, C., Meiburg, E. & Necker, F. 2000b Analysis and direct numerical simulation of the flow at a gravity-current head. Part 1. flow topology and front speed for slip and no-slip boundaries. J. Fluid Mech. 418, 189–212.Google Scholar
Huerre, P. 1983 Finite amplitude evolution of mixing layers in the presence of solid boundaries. J. de Méc. Théor. Appl. 121–145.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing?. Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Lasheras, J. & Choi, H. 1988 3-dimensional instability of a plane free shear-layer - an experimental-study of the formation and evolution of streamwise vortices. J. Fluid Mech. 189, 53–&.Google Scholar
Lawrie, A. & Dalziel, S. 2011a Turbulent diffusion in tall tubes. I. Models for Rayleigh–Taylor instability. Phys. Fluids 23, 085109, doi:10.1063/1.3614477.Google Scholar
Lawrie, A. & Dalziel, S. 2011b Turbulent diffusion in tall tubes. II. Confinement by stratification. Phys. Fluids 23, 085109 DOI: 10.1063/1.3622770.Google Scholar
Linden, P. & Simpson, J. 1986 Gravity-driven flows in a turbulent fluid. J. Fluid Mech. 172, 481–497.Google Scholar
Margolin, L. G., Smolarkiewicz, P. K. & Wyszogradzki, A. A. 2006 Dissipation in implicit turbulence models: a computational study. J. Appl. Mech. 73 (3), 469–473.Google Scholar
Michalke, A. 1964 On the inviscid instability of the hyperbolic tangent velocity profile. J. Fluid Mech. 19 (4), 543–556.Google Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30, 539–578.Google Scholar
Monismith, S., Kimmerer, W., Burau, J. & Stacey, M. 2002 Structure and flow-induced variability of the subtidal salinity field in northern San Francisco Bay. J. Phys. Oceanography 32 (11), 3003–3019.Google Scholar
Peltier, W. & Caulfield, C. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Pierrehumbert, R. & Widnall, S. 1982 The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.Google Scholar
Piotrowski, Z., Smolarkiewicz, P., Malinowski, S. & Wyszogrodzki, A. 2009 On numerical realizability of thermal convection. J. Comput. Phys. 228, 6268–6290.Google Scholar
Shih, L., Koseff, J., Ivey, G. & Ferziger, J. 2005 Parameterization of turbulent fluxes and scales using homogeneous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Simpson, J. E. 1999 Gravity Currents: In the Environment and the Laboratory, 2nd edn. Cambridge University Press.Google Scholar
Waite, M. & Smolarkiewicz, P. 2008 Instability and breakdown of a vertical vortex pair in a strongly stratified fluid. J. Fluid Mech. 606, 239–273.Google Scholar
Winant, C. & Browand, F. 1974 Vortex pairing, the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63, 237–255.Google Scholar
Winters, K., Lombard, P., Riley, J. & D’Asaro, E. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech..Google Scholar
Young, W. 1994 The subinertial mixed-layer approximation. J. Phys. Oceanogr. 24 (8), 1812–1826.Google Scholar