Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mons, Vincent
Du, Yifan
and
Zaki, Tamer A.
2021.
Ensemble-variational assimilation of statistical data in large-eddy simulation.
Physical Review Fluids,
Vol. 6,
Issue. 10,
Conti, Davide
Pettas, Vasilis
Dimitrov, Nikolay
and
Peña, Alfredo
2021.
Wind turbine load validation in wakes using wind field reconstruction techniques and nacelle lidar wind retrievals.
Wind Energy Science,
Vol. 6,
Issue. 3,
p.
841.
Wang, Yunpeng
Yuan, Zelong
Xie, Chenyue
and
Wang, Jianchun
2021.
A dynamic spatial gradient model for the subgrid closure in large-eddy simulation of turbulence.
Physics of Fluids,
Vol. 33,
Issue. 7,
Yuan, Zelong
Wang, Yunpeng
Xie, Chenyue
and
Wang, Jianchun
2021.
Dynamic iterative approximate deconvolution models for large-eddy simulation of turbulence.
Physics of Fluids,
Vol. 33,
Issue. 8,
Wang, Junya
Zhang, Gaofei
and
You, Zheng
2022.
Improved sampling scheme for LiDAR in Lissajous scanning mode.
Microsystems & Nanoengineering,
Vol. 8,
Issue. 1,
Wang, Yunpeng
Yuan, Zelong
Xie, Chenyue
and
Wang, Jianchun
2022.
Temporally sparse data assimilation for the small-scale reconstruction of turbulence.
Physics of Fluids,
Vol. 34,
Issue. 6,
Shapiro, Carl R.
Starke, Genevieve M.
and
Gayme, Dennice F.
2022.
Turbulence and Control of Wind Farms.
Annual Review of Control, Robotics, and Autonomous Systems,
Vol. 5,
Issue. 1,
p.
579.
Li, Jian
Tian, Mengdan
and
Li, Yi
2022.
Synchronizing large eddy simulations with direct numerical simulations via data assimilation.
Physics of Fluids,
Vol. 34,
Issue. 6,
Fang, Liang
Vandewalle, Stefan
and
Meyers, Johan
2022.
A parallel-in-time multiple shooting algorithm for large-scale PDE-constrained optimal control problems.
Journal of Computational Physics,
Vol. 452,
Issue. ,
p.
110926.
Chang, Ning
Yuan, Zelong
and
Wang, Jianchun
2022.
The effect of sub-filter scale dynamics in large eddy simulation of turbulence.
Physics of Fluids,
Vol. 34,
Issue. 9,
Lejeune, Maxime
Moens, Maud
and
Chatelain, Philippe
2022.
A Meandering-Capturing Wake Model Coupled to Rotor-Based Flow-Sensing for Operational Wind Farm Flow Prediction.
Frontiers in Energy Research,
Vol. 10,
Issue. ,
Becker, Marcus
Allaerts, Dries
and
van Wingerden, Jan-Willem
2022.
Ensemble-Based Flow Field Estimation Using the Dynamic Wind Farm Model FLORIDyn.
Energies,
Vol. 15,
Issue. 22,
p.
8589.
Meyers, Johan
Bottasso, Carlo
Dykes, Katherine
Fleming, Paul
Gebraad, Pieter
Giebel, Gregor
Göçmen, Tuhfe
and
van Wingerden, Jan-Willem
2022.
Wind farm flow control: prospects and challenges.
Wind Energy Science,
Vol. 7,
Issue. 6,
p.
2271.
Wang, Yunpeng
Yuan, Zelong
and
Wang, Jianchun
2023.
Ensemble data assimilation-based mixed subgrid-scale model for large-eddy simulations.
Physics of Fluids,
Vol. 35,
Issue. 8,
Mukhatov, Azamat
Le, Tuan-Anh
Do, Ton Duc
and
Pham, Tri T.
2023.
Universal Behavior of the Image Resolution for Different Scanning Trajectories.
Applied System Innovation,
Vol. 6,
Issue. 6,
p.
103.
Letizia, Stefano
Brugger, Peter
Bodini, Nicola
Krishnamurthy, Raghavendra
Scholbrock, Andrew
Simley, Eric
Porté-Agel, Fernando
Hamilton, Nicholas
Doubrawa, Paula
and
Moriarty, Patrick
2023.
Characterization of wind turbine flow through nacelle-mounted lidars: a review.
Frontiers in Mechanical Engineering,
Vol. 9,
Issue. ,
Hasegawa, Yuta
Onodera, Naoyuki
Asahi, Yuuichi
Ina, Takuya
Imamura, Toshiyuki
and
Idomura, Yasuhiro
2023.
Continuous data assimilation of large eddy simulation by lattice Boltzmann method and local ensemble transform Kalman filter (LBM-LETKF).
Fluid Dynamics Research,
Vol. 55,
Issue. 6,
p.
065501.
2023.
Eddy viscosity enhanced temporal direct deconvolution models for temporal large-eddy simulation of turbulence.
Physics of Fluids,
Vol. 35,
Issue. 6,
Chang, Ning
Yuan, Zelong
Wang, Yunpeng
and
Wang, Jianchun
2023.
The effect of filter anisotropy on the large eddy simulation of turbulence.
Physics of Fluids,
Vol. 35,
Issue. 3,
Cobelli, P.
Shukla, K.
Nesmachnow, S.
and
Draper, M.
2023.
Physics informed neural networks for wind field modeling in wind farms.
Journal of Physics: Conference Series,
Vol. 2505,
Issue. 1,
p.
012051.
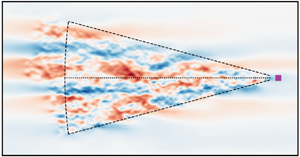
 $15\,\%$ and
$15\,\%$ and  $25\,\%$ (error variance normalised by background variance) in the scanning region, and increase to
$25\,\%$ (error variance normalised by background variance) in the scanning region, and increase to  $100\,\%$ over a distance that is comparable to the correlation length scale outside this scanning region. Moreover, LES outperforms TFT by 30 %–70 % depending on scanning mode and location.
$100\,\%$ over a distance that is comparable to the correlation length scale outside this scanning region. Moreover, LES outperforms TFT by 30 %–70 % depending on scanning mode and location.

