Article contents
Response of a stratified boundary layer on a tilted wall to surface undulations
Published online by Cambridge University Press: 25 June 2014
Abstract
The structure of a stratified boundary layer over a tilted bottom with a small streamwise undulation is studied theoretically and numerically. We show that the tilt of the boundary can induce strong density variations and wall-transverse velocities in the critical layer when the frequency of the forcing by the topography 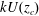 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}kU(z_c)$ is equal to the transverse Brunt–Väisälä frequency
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}kU(z_c)$ is equal to the transverse Brunt–Väisälä frequency 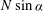 $N \sin \alpha $ (
$N \sin \alpha $ ( 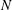 $N$ being the vertical Brunt–Väisälä frequency). The viscous solution in the critical layer, obtained and compared with direct numerical simulation results, is in good agreement for both the scaling and the spatial structure. The amplitude of the transverse velocity response is also shown to exhibit quasi-resonance peaks when the stratification strength is varied.
$N$ being the vertical Brunt–Väisälä frequency). The viscous solution in the critical layer, obtained and compared with direct numerical simulation results, is in good agreement for both the scaling and the spatial structure. The amplitude of the transverse velocity response is also shown to exhibit quasi-resonance peaks when the stratification strength is varied.
Information
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 8
- Cited by

