Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T23:20:44.787Z Has data issue: false hasContentIssue false
  • English
  • Français

A second-order integral model for buoyant jets with background homogeneous and isotropic turbulence

Published online by Cambridge University Press:  20 May 2019

Adrian C. H. Lai Open the ORCID record for Adrian C. H. Lai [Opens in a new window] ,
Adrian Wing-Keung Law Open the ORCID record for Adrian Wing-Keung Law [Opens in a new window]  and
E. Eric Adams Open the ORCID record for E. Eric Adams [Opens in a new window]
Adrian C. H. Lai*
Affiliation:
Environmental Process Modelling Centre, Nanyang Environment and Water Research Institute, Nanyang Technological University, 1 Cleantech Loop, Singapore 637141
Adrian Wing-Keung Law
Affiliation:
Environmental Process Modelling Centre, Nanyang Environment and Water Research Institute, Nanyang Technological University, 1 Cleantech Loop, Singapore 637141 School of Civil and Environmental Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798
E. Eric Adams
Affiliation:
Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: adrianlai@connect.hku.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

Buoyant jets or forced plumes are discharged into a turbulent ambient in many natural and engineering applications. The background turbulence generally affects the mixing characteristics of the buoyant jet, and the extent of the influence depends on the characteristics of both the jet discharge and ambient. Previous studies focused on the experimental investigation of the problem (for pure jets or plumes), but the findings were difficult to generalize because suitable scales for normalization of results were not known. A model to predict the buoyant jet mixing in the presence of background turbulence, which is essential in many applications, is also hitherto not available even for a background of homogeneous and isotropic turbulence (HIT). We carried out experimental and theoretical investigations of a buoyant jet discharging into background HIT. Buoyant jets were designed to be in the range of 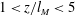$1<z/l_{M}<5$, where 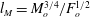$l_{M}=M_{o}^{3/4}/F_{o}^{1/2}$ is the momentum length scale, with 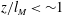$z/l_{M}<\sim 1$ and 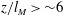$z/l_{M}>\sim 6$ representing the asymptotic cases of pure jets and plumes, respectively. The background turbulence was generated using a random synthetic jet array, which produced a region of approximately isotropic and homogeneous field of turbulence to be used in the experiments. The velocity scale of the jet was initially much higher, and the length scale smaller, than that of the background turbulence, which is typical in most applications. Comprehensive measurements of the buoyant jet mixing characteristics were performed up to the distance where jet breakup occurred. Based on the experimental findings, a critical length scale 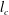$l_{c}$ was identified to be an appropriate normalizing scale. The momentum flux of the buoyant jet in background HIT was found to be conserved only if the second-order turbulence statistics of the jet were accounted for. A general integral jet model including the background HIT was then proposed based on the conservation of mass (using the entrainment assumption), total momentum and buoyancy fluxes, and the decay function of the jet mean momentum downstream. Predictions of jet mixing characteristics from the new model were compared with experimental observation, and found to be generally in agreement with each other.

JFM classification

Wakes/Jets: Jets Convection: Plumes/thermals Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 271 - 304
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Cheng, N. S. & Law, A. W. K. 2001 Measurements of turbulence generated by oscillating grid. J. Hydraul. Engng 127 (3), 201–208.Google Scholar
Ching, C. Y., Fernando, H. J. S. & Robles, A. 1995 Break down of line plumes in turbulent environments. J. Geophys. Res. 100 (C3), 4707–4713.Google Scholar
Craske, J. & van Reeuwijkl, M. 2015 Energy dispersion in turbulent jets. Part 1. Direct simulation of steady and unsteady jets. J. Fluid Mech. 763, 500–537.Google Scholar
Craske, J. & van Reeuwijkl, M. 2016 Generalised unsteady plume theory. J. Fluid Mech. 792, 1013–1052.Google Scholar
Craven, B. A. & Settles, G. S. 2006 A computational and experimental investigation of the human thermal plume. J. Fluids Engng 128 (6), 1251–1258.Google Scholar
Cuthbertson, A. J. S., Malcangio, D., Davies, P. A. & Mossa, M. 2006 The influence of a localized region on turbulence on the structural development of a turbulent, round, buoyant jet. Fluid Dyn. Res. 38, 683–698.Google Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H. 1979 Mixing in Inland and Coastal Waters. Academic Press.Google Scholar
Guo, Y., Malcangio, D., Davies, P. A. & Fernando, H. J. S. 2005 A laboratory investigation into the influence of a localized region on turbulence on the evolution of a round turbulent jet. Fluid Dyn. Res. 36, 78–89.Google Scholar
Hubner, J.2004 Buoyant plumes in a turbulent environment. PhD thesis, University of Cambridge.Google Scholar
Hunt, J. C. R. 1994 Atmospheric jets and plumes. In Recent Research Advances in the Fluid Mechanics of Turbulent Jets and Plumes (ed. Davies, P. A. & Valente Neves, M. I.), NATO ASI Series E, vol. 255, pp. 309–334. Springer.Google Scholar
Hunt, J. C. R., Eames, I. & Westerweel, J. 2006 Mechanics of inhomogeneous turbulence and interfacial layers. J. Fluid Mech. 554, 499–519.Google Scholar
Hussein, H. J., Capp, S. P. & George, W. K. 1994 Velocity measurements in a high-Reynolds-number, momentum-conserving, axisymmetric, turbulent jet. J. Fluid Mech. 258, 31–75.Google Scholar
Khorsandi, B., Gaskin, S. & Mydlarski, L. 2013 Effect of background turbulence on an axisymmetric turbulent jet. J. Fluid Mech. 736, 250–286.Google Scholar
Kiya, M., Ohyama, M. & Hunt, J. C. R. 1986 Vortex pairs and rings interacting with shear layer vortices. J. Fluid Mech. 172, 1–15.Google Scholar
Law, A. W. K., Cheng, N. S. & Davidson, M. J. 2001 Jet spreading in oscillating-grid turbulence. In Proceedings of the 3rd International Symposium on Environmental Hydraulics, vol. 36, pp. 1–6. International Association of Hydro-Environment Engineering and Research (IAHR).Google Scholar
Lee, J. H. W. & Chu, V. H. 2003 Turbulent Jets and Plumes: A Lagrangian Approach. Kluwer.Google Scholar
Linden, P. F. 1999 The fluid mechanics of natural ventilation. Annu. Rev. Fluid Mech. 31, 201–238.Google Scholar
Linden, P. F., Lane-Serff, G. F. & Smeed, D. A. 1990 Emptying filling boxes: the fluid mechanics of natural ventilation. J. Fluid Mech. 212, 309–335.Google Scholar
Loomans, M.1998 The measurement and simulation of indoor airflow. PhD thesis, Technical University of Eindhoven.Google Scholar
Maxey, M. R. 1987 The velocity skewness measured in grid turbulence. Phys. Fluids 30, 935–939.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Papanicolaou, P. N. & List, E. J. 1988 Investigations of round vertical turbulent buoyant jets. J. Fluid Mech. 195, 341–391.Google Scholar
Perez-Alvarado, A.2016 Effect of background turbulence on the scalar field of a turbulent jet. PhD thesis, McGill University.Google Scholar
Petersen, J. E., Sanford, L. P. & Kemp, W. M. 1998 Coastal plankton responses to turbulent mixing in experimental ecosystems. Mar. Ecol. Prog. Ser. 171, 23–41.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
van Reeuwijkl, M. & Craske, J. 2015 Energy-consistent entrainment relations for jets and plumes. J. Fluid Mech. 782, 333–355.Google Scholar
Shabbir, A. & George, W. K. 1994 Experiments on a round turbulent buoyant plume. J. Fluid Mech. 275, 1–32.Google Scholar
Turner, J. S. & Campbell, I. H. 1987 A laboratory and theoretical study of the growth of ‘black smoker’ chimneys. Earth Planet. Sci. Lett. 82, 36–48.Google Scholar
Variano, E. A. & Cowen, E. A. 2008 A random-jet-stirred turbulence tank. J. Fluid Mech. 604, 1–32.Google Scholar
Wang, H. & Law, A. W. K. 2002 Second-order integral model for a round turbulent buoyant jet. J. Fluid Mech. 459, 397–428.Google Scholar
Wood, I. R., Bell, R. G. & Wilkinson, D. L. 1993 Ocean Disposal of Wastewater. World Scientific.Google Scholar
Wright, S. J. 1994 The effect of ambient turbulence on jet mixing. In Recent Research Advances in the Fluid Mechanics of Turbulent Jets and Plumes (ed. Davies, P. A. & Valente Neves, M. I.), NATO ASI Series E, vol. 255, pp. 13–27. Springer.Google Scholar
Zhang, W., He, Z. & Jiang, H. 2017 Scaling for turbulent viscosity of buoyant plumes in stratified fluids: PIV measurement with implications for submarine hydrothermal plume turbulence. Deep-Sea Res. I 129, 89–98.Google Scholar