Article contents
Shock reflection with incident shock–wedge trailing-edge expansion fan interaction
Published online by Cambridge University Press: 04 August 2023
Abstract
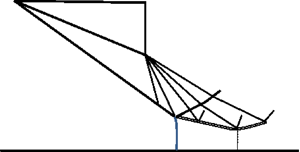
Steady shock reflection where the incident shock is free of interaction with other waves has been well studied. In this paper, we consider the less studied shock reflection problem where the incident shock interacts with the wedge trailing-edge expansion fan, which occurs when the wedge trailing-edge height surpasses a threshold. The influence of this interaction on the advance of transition from Mach reflection to regular reflection is quantified in terms of the wedge trailing-edge height ratio. The wave pattern, including primary and reflected Mach waves, for Mach reflection with interaction is clarified using computational fluid dynamics (CFD) and the method of characteristics. Those reflected Mach waves having an important effect on Mach reflection are identified. A simplified Mach stem model that accounts for the direct role of the interaction on the incident shock and its indirect role on the reflected shock and slipline is built up on a past model without interaction. Both theory and CFD show that the Mach stem height decreases nonlinearly with increasing trailing-edge height.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 4
- Cited by


