Published online by Cambridge University Press: 05 May 2023
Solute dispersion in Carreau–Yasuda fluid flow in a tube presented in Rana & Murthy (Proc. R. Soc. Lond. A, vol. 472, 2016, p. 20160294) was limited to a steady-state velocity profile due to the nonlinearity associated with the Yasuda parameter  $a$ with power-law exponent
$a$ with power-law exponent  $n$. This limitation is overcome and the velocity profile is obtained for all values of the Yasuda parameter by using the Lagrange inversion theorem, which admits power series solution for the flow field. An analytical solution for the concentration distribution in the circular tube is obtained for the unsteady and pulsatile flow with
$n$. This limitation is overcome and the velocity profile is obtained for all values of the Yasuda parameter by using the Lagrange inversion theorem, which admits power series solution for the flow field. An analytical solution for the concentration distribution in the circular tube is obtained for the unsteady and pulsatile flow with  $n\leq 1$ and
$n\leq 1$ and  $\alpha <<1$ and the numerical solution is presented for all values of
$\alpha <<1$ and the numerical solution is presented for all values of  $\alpha$ and
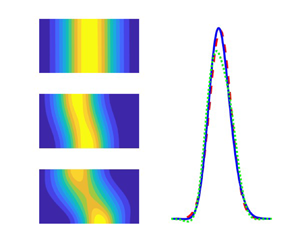
$\alpha$ and  $n$. The solute dispersion is analysed analytically using the Sankarasubramanian–Gill generalized dispersion method and also using the Aris–Barton method of moments considering up to fourth-order moments. The solute dispersion is also simulated numerically by using a new class of computationally explicit Runge–Kutta method. The axial mean concentration of the solute is estimated by the exchange, convective and dispersion coefficients. The third- and fourth-order moments give rise to skewness and kurtosis revealing the deviation from the Gaussianity and reduction in the peak of the mean concentration profile at a small time of the solute injection. All time variations of these five moments against flow governing parameters are thoroughly investigated. The flow and dispersion regimes that are derived here for moments provide a good understanding of the solute dispersion in the tube. The increase in the Womersley frequency parameter led to a phase lag at each period. This work is the initiation of estimating the skewness and kurtosis in a non-yield stress fluid flow in a tube.
$n$. The solute dispersion is analysed analytically using the Sankarasubramanian–Gill generalized dispersion method and also using the Aris–Barton method of moments considering up to fourth-order moments. The solute dispersion is also simulated numerically by using a new class of computationally explicit Runge–Kutta method. The axial mean concentration of the solute is estimated by the exchange, convective and dispersion coefficients. The third- and fourth-order moments give rise to skewness and kurtosis revealing the deviation from the Gaussianity and reduction in the peak of the mean concentration profile at a small time of the solute injection. All time variations of these five moments against flow governing parameters are thoroughly investigated. The flow and dispersion regimes that are derived here for moments provide a good understanding of the solute dispersion in the tube. The increase in the Womersley frequency parameter led to a phase lag at each period. This work is the initiation of estimating the skewness and kurtosis in a non-yield stress fluid flow in a tube.