Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
McConnochie, Craig D.
and
Kerr, Ross C.
2017.
Enhanced ablation of a vertical ice wall due to an external freshwater plume.
Journal of Fluid Mechanics,
Vol. 810,
Issue. ,
p.
429.
McConnochie, C. D.
and
Kerr, R. C.
2017.
Testing a common ice‐ocean parameterization with laboratory experiments.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 7,
p.
5905.
Kaye, N. B.
and
Cooper, P.
2018.
Source and boundary condition effects on unconfined and confined vertically distributed turbulent plumes.
Journal of Fluid Mechanics,
Vol. 850,
Issue. ,
p.
1032.
Ezhova, Ekaterina
Cenedese, Claudia
and
Brandt, Luca
2018.
Dynamics of Three-Dimensional Turbulent Wall Plumes and Implications for Estimates of Submarine Glacier Melting.
Journal of Physical Oceanography,
Vol. 48,
Issue. 9,
p.
1941.
Mondal, Mainak
Gayen, Bishakhdatta
Griffiths, Ross W.
and
Kerr, Ross C.
2019.
Ablation of sloping ice faces into polar seawater.
Journal of Fluid Mechanics,
Vol. 863,
Issue. ,
p.
545.
Porter, David F.
Springer, Scott R.
Padman, Laurie
Fricker, Helen A.
Tinto, Kirsty J.
Riser, Stephen C.
and
Bell, Robin E.
2019.
Evolution of the Seasonal Surface Mixed Layer of the Ross Sea, Antarctica, Observed With Autonomous Profiling Floats.
Journal of Geophysical Research: Oceans,
Vol. 124,
Issue. 7,
p.
4934.
Vreugdenhil, Catherine A.
and
Taylor, John R.
2019.
Stratification Effects in the Turbulent Boundary Layer beneath a Melting Ice Shelf: Insights from Resolved Large-Eddy Simulations.
Journal of Physical Oceanography,
Vol. 49,
Issue. 7,
p.
1905.
Hewitt, Ian J.
2020.
Subglacial Plumes.
Annual Review of Fluid Mechanics,
Vol. 52,
Issue. 1,
p.
145.
He, Guoqing
2020.
A general model for predicting the airflow rates of a vertically installed solar chimney with connecting ducts.
Energy and Buildings,
Vol. 229,
Issue. ,
p.
110481.
Gwyther, David E.
Kusahara, Kazuya
Asay-Davis, Xylar S.
Dinniman, Michael S.
and
Galton-Fenzi, Benjamin K.
2020.
Vertical processes and resolution impact ice shelf basal melting: A multi-model study.
Ocean Modelling,
Vol. 147,
Issue. ,
p.
101569.
Chong, Kai Leong
Yang, Rui
Wang, Qi
Verzicco, Roberto
and
Lohse, Detlef
2020.
Café latte: spontaneous layer formation in laterally cooled double diffusive convection.
Journal of Fluid Mechanics,
Vol. 900,
Issue. ,
Malyarenko, Alena
Wells, Andrew J.
Langhorne, Patricia J.
Robinson, Natalie J.
Williams, Michael J.M.
and
Nicholls, Keith W.
2020.
A synthesis of thermodynamic ablation at ice–ocean interfaces from theory, observations and models.
Ocean Modelling,
Vol. 154,
Issue. ,
p.
101692.
Noble, T. L.
Rohling, E. J.
Aitken, A. R. A.
Bostock, H. C.
Chase, Z.
Gomez, N.
Jong, L. M.
King, M. A.
Mackintosh, A. N.
McCormack, F. S.
McKay, R. M.
Menviel, L.
Phipps, S. J.
Weber, M. E.
Fogwill, C. J.
Gayen, B.
Golledge, N. R.
Gwyther, D. E.
Hogg, A. McC.
Martos, Y. M.
Pena‐Molino, B.
Roberts, J.
van de Flierdt, T.
and
Williams, T.
2020.
The Sensitivity of the Antarctic Ice Sheet to a Changing Climate: Past, Present, and Future.
Reviews of Geophysics,
Vol. 58,
Issue. 4,
Vreugdenhil, Catherine A.
and
Gayen, Bishakhdatta
2021.
Ocean Convection.
Fluids,
Vol. 6,
Issue. 10,
p.
360.
Parker, D. A.
Burridge, H. C.
Partridge, J. L.
and
Linden, P. F.
2021.
Vertically distributed wall sources of buoyancy. Part 1. Unconfined.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
Couston, Louis-Alexandre
Hester, Eric
Favier, Benjamin
Taylor, John R.
Holland, Paul R.
and
Jenkins, Adrian
2021.
Topography generation by melting and freezing in a turbulent shear flow.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
Ke, Junhao
Williamson, N.
Armfield, S.W.
Komiya, A.
and
Norris, S.E.
2021.
High Grashof number turbulent natural convection on an infinite vertical wall.
Journal of Fluid Mechanics,
Vol. 929,
Issue. ,
Rosevear, Madelaine Gamble
Gayen, Bishakhdatta
and
Galton-Fenzi, Benjamin Keith
2021.
The role of double-diffusive convection in basal melting of Antarctic ice shelves.
Proceedings of the National Academy of Sciences,
Vol. 118,
Issue. 6,
Lopes, José Fortes
2022.
Using Different Classic Turbulence Closure Models to Assess Salt and Temperature Modelling in a Lagunar System: A Sensitivity Study.
Journal of Marine Science and Engineering,
Vol. 10,
Issue. 11,
p.
1750.
Na, Ji Sung
Kim, Taekyun
Jin, Emilia Kyung
Yoon, Seung-Tae
Lee, Won Sang
Yun, Sukyoung
and
Lee, Jiyeon
2022.
Large-eddy simulations of the ice-shelf–ocean boundary layer near the ice front of Nansen Ice Shelf, Antarctica.
The Cryosphere,
Vol. 16,
Issue. 9,
p.
3451.
 $-1\,^{\circ }\text{C}$ and
$-1\,^{\circ }\text{C}$ and 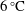 $6\,^{\circ }\text{C}$ and salinities around 35 ‰, where diffusion of salt to the ice–water interface depresses the freezing point and enhances heat diffusion to the ice. We show that fluxes of both heat and salt to the interface are significant in governing the dissolution of ice, and the ablation velocity agrees well with experiments and a recent theoretical prediction. The same turbulent flow dynamics and ablation rate are expected to apply at any depth in a deeper ocean water column (after choosing the relevant pressure coefficient for the liquidus temperature). At Grashof numbers currently accessible by direct numerical simulation, turbulence is generated both directly from buoyancy flux and from shear production in the buoyancy-driven boundary layer flow, whereas shear production by the convective flow is expected to be more important at geophysical scales. The momentum balance in the boundary layer is dominated by buoyancy forcing and wall stress, with the latter characterised by a large drag coefficient.
$6\,^{\circ }\text{C}$ and salinities around 35 ‰, where diffusion of salt to the ice–water interface depresses the freezing point and enhances heat diffusion to the ice. We show that fluxes of both heat and salt to the interface are significant in governing the dissolution of ice, and the ablation velocity agrees well with experiments and a recent theoretical prediction. The same turbulent flow dynamics and ablation rate are expected to apply at any depth in a deeper ocean water column (after choosing the relevant pressure coefficient for the liquidus temperature). At Grashof numbers currently accessible by direct numerical simulation, turbulence is generated both directly from buoyancy flux and from shear production in the buoyancy-driven boundary layer flow, whereas shear production by the convective flow is expected to be more important at geophysical scales. The momentum balance in the boundary layer is dominated by buoyancy forcing and wall stress, with the latter characterised by a large drag coefficient.

