Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-10T09:41:50.881Z Has data issue: false hasContentIssue false
  • English
  • Français

The spontaneous puncture of thick liquid films

Published online by Cambridge University Press:  12 January 2018

B. Néel  and
E. Villermaux Open the ORCID record for E. Villermaux [Opens in a new window]
B. Néel
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, Marseille, France
E. Villermaux*
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE, Marseille, France Institut Universitaire de France, Paris, France
*
†Email address for correspondence: villermaux@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

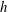We call thick those films for which the disjoining pressure and thermal fluctuations are ineffective. Water films with thickness $h$ in the 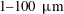$1{-}100~\unicode[STIX]{x03BC}\text{m}$ range are thick, but are also known, paradoxically, to nucleate holes spontaneously. We have uncovered a mechanism solving the paradox, relying on the extreme sensitivity of the film to surface tension inhomogeneities. The surface tension of a free liquid film is lowered by an amount 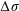$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}$ over a size $a$ by chemical or thermal contamination. At the same time this spot diffuses (within a time 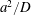$a^{2}/D$, with 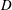$D$ the diffusion coefficient of the pollutant in the substrate), the Marangoni stress 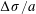$\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}/a$ induces an inhomogeneous outward interstitial flow which digs the film within a time 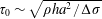$\unicode[STIX]{x1D70F}_{0}\sim \sqrt{\unicode[STIX]{x1D70C}ha^{2}/\unicode[STIX]{x0394}\unicode[STIX]{x1D70E}}$, with 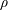$\unicode[STIX]{x1D70C}$ the density of the liquid. When the Péclet number 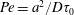$Pe=a^{2}/D\unicode[STIX]{x1D70F}_{0}$ is larger than unity, the liquid substrate motion reinforces the surface tension gradient, triggering a self-sustained instability insensitive to diffusional regularisation. Several experimental illustrations of the phenomenon are given, both qualitative and quantitative, including a precise study of the first instants of the unstable dynamics made by controlled perturbations of a Savart sheet at large 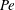$Pe$.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Drops and Bubbles: Thermocapillarity Interfacial Flows (free surface): Thin films
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 838 , 10 March 2018 , pp. 192 - 221
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113–133.Google Scholar
Berendsen, C. W. J., Zeegers, J. C. H., Kruis, G. C. F. L., Riepen, M. & Darhuber, A. A. 2012 Rupture of thin liquid films induced by impinging air-jets. Langmuir 28 (26), 9977–9985.Google Scholar
Betterton, M. D. & Brenner, M. P. 1999 Electrostatic edge instability of lipid membranes. Phys. Rev. Lett. 82 (7), 1598–1601.CrossRefGoogle Scholar
Blanchard, D. C. 1963 The electrification of the atmosphere by particles from bubbles in the sea. Prog. Oceanogr. 1, 73–202.Google Scholar
Boos, W. & Thess, A. 1999 Cascade of structures in long-wavelength Marangoni instability. Phys. Fluids 11 (6), 1484–1494.CrossRefGoogle Scholar
Bowen, M. & Tilley, B. S. 2013 On self-similar thermal rupture of thin liquid sheets. Phys. Fluids 25, 102105.Google Scholar
Bremond, N. & Villermaux, E. 2005 Bursting thin liquid films. J. Fluid Mech. 524, 121–130.Google Scholar
Burton, J. C. & Taborek, P. 2007 Two-dimensional inviscid pinch-off: an example of self-similarity of the second kind. Phys. Fluids 19, 102109.Google Scholar
Casteletto, V., Cantat, I., Sarker, D., Bausch, R., Bonn, D. & Meunier, J. 2003 Stability of soap films: hysteresis and nucleation of black films. Phys. Rev. Lett. 90, 048302.Google Scholar
Champougny, L., Rio, E., Restagno, F. & Scheid, B. 2017 The break-up of free films pulled out of a pure liquid bath. J. Fluid Mech. 811, 499–524.CrossRefGoogle Scholar
Clanet, C. & Villermaux, E. 2002 Life of a smooth liquid sheet. J. Fluid Mech. 462, 307–340.Google Scholar
Courbin, L. & Stone, H. A. 2006 Impact, puncturing, and the self-healing of soap films. Phys. Fluids 18, 091105.Google Scholar
Craster, R. V. & Matar, O. K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81 (3), 1131–1198.CrossRefGoogle Scholar
Culick, F. E. C. 1960 Comments on a ruptured soap film. J. Appl. Phys. 31, 1128–1129.Google Scholar
Denkov, N. D. 2004 Mechanisms of foam destruction by oil-based antifoams. Langmuir 20 (22), 9463–9505.Google Scholar
Derjaguin, B. V., Churaev, N. V. & Muller, V. M. 1987 Surface Forces. Plenum.Google Scholar
Dombrowski, N. & Fraser, R. P. 1954 A photographic investigation into the disintegration of liquid sheets. Phil. Trans. R. Soc. Lond. A 247, 101–130.Google Scholar
Duchemin, L., Le Dizès, S., Vincent, L. & Villermaux, E. 2015 Self-similar impulsive capillary waves on a ligament. Phys. Fluids 27, 051704.CrossRefGoogle Scholar
Enders, S., Kahl, H. & Winkelmann, J. 2007 Surface tension of the ternary system water + acetone + toluene. J. Chem. Engng Data 52 (3), 1072–1079.CrossRefGoogle Scholar
Erneux, T. & Davis, S. H. 1993 Nonlinear rupture of free films. Phys. Fluids A 5 (5), 1117–1122.Google Scholar
Fowler, R. & Guggenheim, E. A. 1952 Statistical Thermodynamics. Cambridge University Press.Google Scholar
Frank-Kamenetskii, D. A. 1969 Diffusion and Heat Transfer in Chemical Kinetics. Plenum.Google Scholar
Garrett, P. R. 1992 Defoaming: Theory and Industrial Applications, Surfactant Science Series 45. Taylor & Francis.Google Scholar
de Gennes, P.-G. 1998 Progression d’un agent de coalescence dans une émulsion. C. R. Acad. Sci. Paris IIb 326, 331–335.Google Scholar
Gordillo, J. M., Lhuissier, H. & Villermaux, E. 2014 On the cusps bordering liquid sheets. J. Fluid Mech. 754, R1.Google Scholar
Guéna, G., Poulard, C. & Cazabat, A.-M. 2007 Evaporating drops of alkane mixtures. Colloids Surf. Physicochem. Engng Asp. 298 (1–2), 2–11.Google Scholar
Hernández-Sánchez, J. F., Eddi, A. & Snoeijer, J. H. 2015 Marangoni spreading due to a localized alcohol supply on a thin water film. Phys. Fluids 27, 032003.Google Scholar
Huang, J. C. P. 1970 The break-up of axisymmetric liquid sheets. J. Fluid Mech. 43, 305–319.Google Scholar
Ilton, M., Dimaria, C. & Dalnoki-Veress, K. 2016 Direct measurement of the critical pore size in a model membrane. Phys. Rev. Lett. 117, 257801.Google Scholar
Isenberg, C. 1992 The Science of Soap Films and Soap Bubbles. Dover.Google Scholar
Israelachvili, J. N. 1991 Intermolecular and Surface Forces, 2nd edn. Academic Press.Google Scholar
Jacob, F. 1987 La Statue Intérieure. Editions Odile Jacob, Seuil.Google Scholar
Jensen, O. E. & Grotberg, J. B. 1992 Insoluble surfactant spreading on a thin viscous film: shock evolution and film rupture. J. Fluid Mech. 240, 259–288.CrossRefGoogle Scholar
Jensen, O. E. & Grotberg, J. B. 1993 The spreading of heat or soluble surfactant along a thin liquid film. Phys. Fluids A 5 (1), 58–68.Google Scholar
Kabova, Y. O., Alexeev, A., Gambaryan-Roisman, T. & Stephan, P. 2006 Marangoni-induced deformation and rupture of a liquid film on a heated microstructured wall. Phys. Fluids 18, 012104.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M. G. 2012 Falling Liquid Films. Springer.Google Scholar
Leenaars, A. F. M., Huethorst, J. A. M. & Van Oekel, J. J. 1990 Marangoni drying: a new extremely clean drying process. Langmuir 6 (11), 1701–1703.CrossRefGoogle Scholar
Levich, V. G. & Krylov, V. S. 1969 Surface-tension-driven phenomena. Annu. Rev. Fluid Mech. 1, 293–316.CrossRefGoogle Scholar
Lhuissier, H., Brunet, P. & Dorbolo, S. 2016 Blowing a liquid curtain. J. Fluid Mech. 795, 784–807.Google Scholar
Lhuissier, H. & Villermaux, E. 2009a Destabilization of flapping sheets: the surprising analogue of soap films. C. R. Méc. 337, 469–480.CrossRefGoogle Scholar
Lhuissier, H. & Villermaux, E. 2009b Soap films burst like flapping flags. Phys. Rev. Lett. 103, 054501.Google Scholar
Lhuissier, H. & Villermaux, E. 2011 The destabilization of an initially thick liquid sheet edge. Phys. Fluids 23, 091705.CrossRefGoogle Scholar
Lhuissier, H. & Villermaux, E. 2012a Bursting bubble aerosols. J. Fluid Mech. 696, 5–44.Google Scholar
Lhuissier, H. & Villermaux, E. 2012b Crumpled water bells. J. Fluid Mech. 693, 508–540.Google Scholar
Lhuissier, H. & Villermaux, E. 2013 ‘Effervescent’ atomization in two dimensions. J. Fluid Mech. 714, 361–392.Google Scholar
Lide, D. R.(Ed.) 2010 CRC Handbook of Chemistry and Physics, 90th edn. CRC Press/Taylor & Francis.Google Scholar
Linstrom, P. J. & Mallard, W. G.(Eds) 2017 NIST Chemistry WebBook (NIST Standard Reference Database 69) , National Institute of Standards and Technology.Google Scholar
Marangoni, C. 1878 Difesa della teoria dell’elasticità superficiale dei liquidi: plasticità superficiale. Il Nuovo Cimento 3 III (3), 193–211.CrossRefGoogle Scholar
Marmottant, P., Villermaux, E. & Clanet, C. 2000 Transient surface tension of an expanding liquid sheet. J. Colloid Interface Sci. 230 (1), 29–40.CrossRefGoogle ScholarPubMed
Matar, O. K. & Craster, R. V. 2001 Models for Marangoni drying. Phys. Fluids 13 (7), 1869–1883.Google Scholar
Maxwell, J. C. 1875 Capillary Action, 9th edn. Encyclopedia Britannica.Google Scholar
McEntee, W. R. & Mysels, K. J. 1969 The bursting of soap films. Part I. An experimental study. J. Phys. Chem. 73 (9), 3018–3028.Google Scholar
Nierstrasz, V. A. & Frens, G. 1998 Marginal regeneration in thin vertical liquid films. J. Colloid Interface Sci. 207 (2), 209–217.Google Scholar
Pratt, K. C. & Wakeham, W. A. 1975 The mutual diffusion coefficient for binary mixtures of water and the isomers of propanol. Proc. R. Soc. Lond. Math. Phys. Engng Sci. 342 (1630), 401–419.Google Scholar
Ranz, W. E. 1959 Some experiments on the dynamics of liquid films. J. Appl. Phys. 30 (12), 1950–1955.CrossRefGoogle Scholar
Ranz, W. E. 1979 Applications of a stretch model to mixing, diffusion, and reaction in laminar and turbulent flows. AIChE J. 25 (1), 41–47.Google Scholar
Reiter, G. 1992 Dewetting of thin polymer films. Phys. Rev. Lett. 68 (1), 75–78.Google Scholar
de Rivas, A. & Villermaux, E. 2016 Dense spray evaporation as a mixing process. Phys. Rev. Fluids 1, 014201.Google Scholar
Roché, M., Li, Z., Griffiths, I. M., Le Roux, S., Cantat, I., Saint-Jalmes, A. & Stone, H. A. 2014 Marangoni flow of soluble amphiphiles. Phys. Rev. Lett. 112, 208302.Google Scholar
Savart, F. 1833 Mémoire sur le choc d’une veine liquide lancée contre un plan circulaire. Ann. Chim. Phys. 54, 55–87.Google Scholar
Scriven, L. E. & Sternling, C. V. 1960 The Marangoni effects. Nature 187 (4733), 186–188.Google Scholar
Settles, G. S. 2001 Schlieren and Shadowgraph Techniques. Springer.Google Scholar
Sharma, A. & Reiter, G. 1996 Instability of thin polymer films on coated substrates: rupture, dewetting, and drop formation. J. Colloid Interface Sci. 178 (2), 383–399.Google Scholar
Taylor, G. I. 1959a The dynamics of thin sheets of fluid. Part II. waves on fluid sheets. Proc. R. Soc. Lond. A 253, 296–312.Google Scholar
Taylor, G. I. 1959b The dynamics of thin sheets of fluid. Part III. Disintegration of fluid sheets. Proc. R. Soc. Lond. A 253, 313–321.Google Scholar
Taylor, G. I. & Michael, D. H. 1973 On making holes in a sheet of fluid. J. Fluid Mech. 58, 625–639.Google Scholar
Thoroddsen, S. T., Etoh, T. G. & Takehara, K. 2006 Crown breakup by Marangoni instability. J. Fluid Mech. 557, 63–72.Google Scholar
Thoroddsen, S. T., Thoraval, M.-J., Takehara, K. & Etoh, T. G. 2012 Micro-bubble morphologies following drop impacts onto a pool surface. J. Fluid Mech. 708, 469–479.Google Scholar
Vanhook, S. J., Schatz, M. F., Swift, J. B., McCormick, W. D. & Swinney, H. L. 1997 Long-wavelength surface-tension-driven Bénard convection: experiment and theory. J. Fluid Mech. 345, 45–78.Google Scholar
Vargaftik, N. B., Vinogradov, Y. K. & Yargin, V. S. 1996 Handbook of Physical Properties of Liquids and Gases: New Augmented and Revised Edition of the Classic Reference. Begell House.Google Scholar
Vargaftik, N. B., Volkov, B. N. & Voljak, L. D. 1983 International tables of the surface tension of water. J. Phys. Chem. Ref. Data 12 (3), 817–820.Google Scholar
Vazquez, G., Alvarez, E. & Navaza, J. M. 1995 Surface tension of alcohol water + water from 20 to 50 °C. J. Chem. Engng Data 40 (3), 611–614.Google Scholar
Vernay, C., Ramos, L. & Ligoure, C. 2015 Bursting of dilute emulsion-based liquid sheets driven by a Marangoni effect. Phys. Rev. Lett. 115, 198302.Google Scholar
Villermaux, E. 2012 On dissipation in stirred mixtures. Adv. Appl. Mech. 45, 91–107.Google Scholar
Villermaux, E. & Almarcha, C. 2016 Node dynamics and cusps size distribution at the border of liquid sheets. Phys. Rev. Fluids 1, 041902.CrossRefGoogle Scholar
Villermaux, E. & Clanet, C. 2002 Life of a flapping liquid sheet. J. Fluid Mech. 462.Google Scholar
Villermaux, E. & Duplat, J. 2003 Mixing as an aggregation process. Phys. Rev. Lett. 91, 184501.Google Scholar
Villermaux, E., Pistre, V. & Lhuissier, H. 2013 The viscous Savart sheet. J. Fluid Mech. 730, 607–625.Google Scholar
Vledouts, A., Quinard, J., Vandenberghe, N. & Villermaux, E. 2016 Explosive fragmentation of liquid shells. J. Fluid Mech. 788, 246–273.Google Scholar
Vrij, A. 1966 Possible mechanism for the spontaneous rupture of thin, free liquid films. Discuss. Faraday Soc. 42, 23–33.Google Scholar
Wedershoven, H. M. J. M., Berendsen, C. W. J., Zeegers, J. C. H. & Darhuber, A. A. 2015 Infrared-laser-induced thermocapillary deformation and destabilization of thin liquid films on moving substrates. Phys. Rev. Appl. 3, 024005.Google Scholar
Worthington, A. M. 1908 A Study of Splashes. Longmans, Green & Co.Google Scholar
Zeldovich, Y. B., Barenblatt, G. I., Librovich, V. B. & Makhviladze, G. M. 1985 The Mathematical Theory of Combustion and Explosions. Consultants Bureau.Google Scholar