Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Sengupta, Sourav
and
De, Sirshendu
2019.
Stability of Poiseuille flow of a Bingham fluid overlying an anisotropic and inhomogeneous porous layer.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
573.
Sengupta, Sourav
and
De, Sirshendu
2019.
Couette–Poiseuille flow of a Bingham fluid through a channel overlying a porous layer.
Journal of Non-Newtonian Fluid Mechanics,
Vol. 265,
Issue. ,
p.
28.
Sengupta, Sourav
and
De, Sirshendu
2020.
Effect of Couette component on the stability of Poiseuille flow of a Bingham fluid–porous system: Modal and non-modal approaches.
Physics of Fluids,
Vol. 32,
Issue. 6,
Shankar, B. M.
Shivakumara, I. S.
and
Kumar, Jai
2020.
Benchmark solution for the hydrodynamic stability of plane porous-Couette flow.
Physics of Fluids,
Vol. 32,
Issue. 10,
Samanta, Arghya
2020.
Linear stability of a plane Couette–Poiseuille flow overlying a porous layer.
International Journal of Multiphase Flow,
Vol. 123,
Issue. ,
p.
103160.
K., Srinivas Kirthy
and
Diwan, Sourabh S.
2021.
Energy budget analysis and neutral curve characteristics for the linear instability of Couette–Poiseuille flow.
Physics of Fluids,
Vol. 33,
Issue. 3,
Sengupta, Sourav
and
De, Sirshendu
2021.
Long-time instability and transient behavior of pressure-driven flow of a power-law fluid in a plane channel overlying a porous layer.
Physics of Fluids,
Vol. 33,
Issue. 5,
Sengupta, Sourav
and
De, Sirshendu
2021.
Effect of the transition layer on the stability of a fluid-porous configuration: Impact on power-law rheology.
Physical Review Fluids,
Vol. 6,
Issue. 6,
Shankar, B. M.
and
Shivakumara, I. S.
2021.
Changes in the hydrodynamic stability of plane porous-Couette flow due to vertical throughflow.
Physics of Fluids,
Vol. 33,
Issue. 7,
Karmakar, Supriya
Usha, R.
Chattopadhyay, Geetanjali
Millet, Severine
Ramana Reddy, J. V.
and
Shukla, Priyanka
2022.
Stability of a plane Poiseuille flow in a channel bounded by anisotropic porous walls.
Physics of Fluids,
Vol. 34,
Issue. 3,
Anjali
Khan, Arshan
and
Bera, P.
2022.
Stability of non-isothermal Poiseuille flow in a fluid overlying an anisotropic and inhomogeneous porous domain.
Journal of Fluid Mechanics,
Vol. 949,
Issue. ,
Hooshyar, Saman
Yoshikawa, Harunori N.
and
Mirbod, Parisa
2022.
The impact of imposed Couette flow on the stability of pressure-driven flows over porous surfaces.
Journal of Engineering Mathematics,
Vol. 132,
Issue. 1,
Samanta, Arghya
2023.
Modal analysis of a fluid flowing over a porous substrate.
Theoretical and Computational Fluid Dynamics,
Vol. 37,
Issue. 2,
p.
241.
Barman, N.
Aleria, A.
and
Bera, P.
2024.
Can isothermal plane Couette flow in fluid overlying porous layer be linearly unstable?.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Peng, Haiwen
Hu, Hongwei
Ding, Jiali
Cheng, Guanggui
and
Ding, Jianning
2024.
Enhancing uniformity in large-area slot die coating of low-viscosity perovskite ink.
Journal of Coatings Technology and Research,
Vol. 21,
Issue. 5,
p.
1649.
Barman, N.
Aleria, A.
and
Bera, P.
2024.
Non-Isothermal Plane Couette Flow and Its Stability in an Anisotropic and Inhomogeneous Porous Layer Underlying a Fluid Layer Saturated by Water.
ASME Journal of Heat and Mass Transfer,
Vol. 146,
Issue. 7,
Roy, Monisha
Ghosh, Sukhendu
and
Raja Sekhar, G.P.
2024.
Linear stability analysis of a Couette-Poiseuille flow: A fluid layer overlying an anisotropic and inhomogeneous porous layer.
Computers & Mathematics with Applications,
Vol. 173,
Issue. ,
p.
102.
Sharma, Ajay
Aleria, Anjali
and
Bera, P.
2024.
Stability analysis of Poiseuille flow in an annulus partially filled with porous medium.
Physics of Fluids,
Vol. 36,
Issue. 2,
Cui, Jianzhong
and
Tang, Hui
2024.
A review on flow instability in hydro-viscous drive.
Physics of Fluids,
Vol. 36,
Issue. 4,
Sharma, Ajay
Bera, P.
and
Sharma, Gaurav
2025.
Hagen–Poiseuille flow in the pipe layered by porous medium is linearly unstable.
International Journal of Multiphase Flow,
Vol. 189,
Issue. ,
p.
105243.
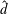 $\hat{d}$ , defined by the ratio of the depth of the fluid layer to the depth of the porous layer, and induce a tri-modal structure to the neutral curves. At moderate
$\hat{d}$ , defined by the ratio of the depth of the fluid layer to the depth of the porous layer, and induce a tri-modal structure to the neutral curves. At moderate 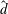 $\hat{d}$ , the Couette component generally produces a stabilization effect on the flow. When the velocity of the upper moving wall is large enough, a bi-modal behaviour of the neutral curves appears and a shift of instability mode occurs from the long-wave fluid-layer mode to the porous-layer mode with higher wavenumber. These stability characteristics are remarkably different from those of the plane Poiseuille–Couette flow in a single fluid layer in that the flow becomes absolutely stable when the wall velocity is over 70 % of the maximum velocity of the Poiseuille component of flow. The stability of pure Couette flow in such a two-layer system is also studied. It is found that the flow is still absolutely stable with respect to infinitesimal disturbances, which is the same as the stability characteristic of a single-layer plane Couette flow.
$\hat{d}$ , the Couette component generally produces a stabilization effect on the flow. When the velocity of the upper moving wall is large enough, a bi-modal behaviour of the neutral curves appears and a shift of instability mode occurs from the long-wave fluid-layer mode to the porous-layer mode with higher wavenumber. These stability characteristics are remarkably different from those of the plane Poiseuille–Couette flow in a single fluid layer in that the flow becomes absolutely stable when the wall velocity is over 70 % of the maximum velocity of the Poiseuille component of flow. The stability of pure Couette flow in such a two-layer system is also studied. It is found that the flow is still absolutely stable with respect to infinitesimal disturbances, which is the same as the stability characteristic of a single-layer plane Couette flow.

