Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-15T01:28:55.756Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic fluid structure interaction of three-dimensional plates facing a uniform flow

Published online by Cambridge University Press:  05 April 2016

O. Cadot
O. Cadot*
Affiliation:
IMSIA, ENSTA-ParisTech/CNRS/CEA/EDF, Université Paris Saclay, 828 Boulevard des Maréchaux, 91762 Palaiseau CEDEX, France
*
†Email address for correspondence: cadot@ensta.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

An experiment on a flat rectangular plate facing a uniform flow at 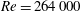$Re=264\,000$ shows the importance of the base pressure loading on the asymmetric static modes of the turbulent wake. The plate is free to rotate around its short symmetry axis. For plates with aspect ratio 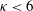${\it\kappa}<6$, the angular position exhibits strong random discontinuities between steady states of non-zero angles. The steady states have long time durations, more than one order of magnitude greater than the convective time scale. The discontinuities, comparable to rare and violent events, are due to strong fluid forces associated with a drastic global change of the three-dimensional wake – mainly the switching between the static asymmetric modes. A clear transition occurs at 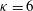${\it\kappa}=6$, for which the angular fluctuations are minimum, leading for 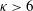${\it\kappa}>6$ to a classical fluid structure interaction with periodic fluctuations. The transition is supported by a recent global stability analysis of rectangular fixed plates in the laminar regime.

JFM classification

Aerodynamics: Aerodynamics
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , R1
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bohorquez, P., Sanmiguel-Rojas, E., Sevilla, A., Jiménez-González, J. I. & Martínez-Bazán, C. 2011 Stability and dynamics of the laminar wake past a slender blunt-based axisymmetric body. J. Fluid Mech. 676 (1), 110–144.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2012 Wake-induced oscillatory paths of bodies freely rising or falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2012 Reflectional symmetry breaking of the separated flow over three-dimensional bluff bodies. Phys. Rev. E 86, 035302.Google Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2013 Turbulent wake past a three-dimensional blunt body. Part 1. Global modes and bi-stability. J. Fluid Mech. 722, 51–84.CrossRefGoogle Scholar
Grandemange, M., Gohlke, M. & Cadot, O. 2014 Statistical axisymmetry of the turbulent sphere wake. Exp. Fluids 55 (11), 1–10.CrossRefGoogle Scholar
Marquet, O. & Larsson, M. 2014 Global wake instabilities of low aspect-ratio flat-plates. Eur. J. Mech. (B/Fluids) 49, 400–412.CrossRefGoogle Scholar
Pier, B. 2008 Local and global instabilities in the wake of a sphere. J. Fluid Mech. 603, 39–61.CrossRefGoogle Scholar
Rigas, G., Morgans, A. S., Brackston, R. D. & Morrison, J. F. 2015 Diffusive dynamics and stochastic models of turbulent axisymmetric wakes. J. Fluid Mech. 778, R2.CrossRefGoogle Scholar
Rigas, G., Oxlade, A. R., Morgans, A. S. & Morrison, J. F. 2014 Low-dimensional dynamics of a turbulent axisymmetric wake. J. Fluid Mech. 755, 159.Google Scholar
Wu, T. 1956 A free streamline theory for two-dimensional fully cavitated hydrofoils. J. Math. Phys. 35 (1), 236–265.CrossRefGoogle Scholar