Article contents
Strong wave–mean-flow coupling in baroclinic acoustic streaming
Published online by Cambridge University Press: 06 November 2018
Abstract
The interaction of an acoustic wave with a stratified fluid can drive strong streaming flows owing to the baroclinic production of fluctuating vorticity, as recently demonstrated by Chini et al. (J. Fluid Mech., 744, 2014, pp. 329–351). In the present investigation, a set of wave/mean-flow interaction equations is derived that governs the coupled dynamics of a standing acoustic-wave mode of characteristic (small) amplitude  $\unicode[STIX]{x1D716}$ and the streaming flow it drives in a thin channel with walls maintained at differing temperatures. Unlike classical Rayleigh streaming, the resulting mean flow arises at
$\unicode[STIX]{x1D716}$ and the streaming flow it drives in a thin channel with walls maintained at differing temperatures. Unlike classical Rayleigh streaming, the resulting mean flow arises at 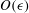 $O(\unicode[STIX]{x1D716})$ rather than at
$O(\unicode[STIX]{x1D716})$ rather than at 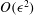 $O(\unicode[STIX]{x1D716}^{2})$. Consequently, fully two-way coupling between the waves and the mean flow is possible: the streaming is sufficiently strong to induce
$O(\unicode[STIX]{x1D716}^{2})$. Consequently, fully two-way coupling between the waves and the mean flow is possible: the streaming is sufficiently strong to induce 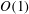 $O(1)$ rearrangements of the imposed background temperature and density fields, which modifies the spatial structure and frequency of the acoustic mode on the streaming time scale. A novel Wentzel–Kramers–Brillouin–Jeffreys analysis is developed to average over the fast wave dynamics, enabling the coupled system to be integrated strictly on the slow time scale of the streaming flow. Analytical solutions of the reduced system are derived for weak wave forcing and are shown to reproduce results from prior direct numerical simulations (DNS) of the compressible Navier–Stokes and heat equations with remarkable accuracy. Moreover, numerical simulations of the reduced system are performed in the regime of strong wave/mean-flow coupling for a fraction of the computational cost of the corresponding DNS. These simulations shed light on the potential for baroclinic acoustic streaming to be used as an effective means to enhance heat transfer.
$O(1)$ rearrangements of the imposed background temperature and density fields, which modifies the spatial structure and frequency of the acoustic mode on the streaming time scale. A novel Wentzel–Kramers–Brillouin–Jeffreys analysis is developed to average over the fast wave dynamics, enabling the coupled system to be integrated strictly on the slow time scale of the streaming flow. Analytical solutions of the reduced system are derived for weak wave forcing and are shown to reproduce results from prior direct numerical simulations (DNS) of the compressible Navier–Stokes and heat equations with remarkable accuracy. Moreover, numerical simulations of the reduced system are performed in the regime of strong wave/mean-flow coupling for a fraction of the computational cost of the corresponding DNS. These simulations shed light on the potential for baroclinic acoustic streaming to be used as an effective means to enhance heat transfer.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 19
- Cited by



