Published online by Cambridge University Press: 22 August 2017
We investigate the flow and turbulence structure in front of a cylinder mounted on a flat plate by a combined study using highly resolved large-eddy simulation and particle image velocimetry. The Reynolds number based on the bulk velocity and cylinder diameter is 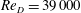 $Re_{D}=39\,000$. As the cylinder is placed in an open channel, we take special care to simulate open-channel flow as the inflow condition, including secondary flows that match the inflow in the experiment. Due to the high numerical resolution, subgrid contributions to the Reynolds stresses are negligible and the modelled dissipation plays a minor role in major parts of the flow field. The accordance of the experimental and numerical results is good. The shear in the approach flow creates a vertical pressure gradient, inducing a downflow in the cylinder front. This downflow, when deflected in the upstream direction at the bottom plate, gives rise to a so-called horseshoe vortex system. The most upstream point of flow reversal at the wall is found to be a stagnation point which appears as a sink instead of a separation point in the symmetry plane in front of the cylinder. The wall shear stress is largest between the main (horseshoe) vortex and the cylinder, and seems to be mainly governed by the strong downflow in front of the cylinder as turbulent stresses are small in this region. Due to a strong acceleration along the streamlines, a region of relatively small turbulent kinetic energy is found between the horseshoe vortex and the cylinder. When passing under the horseshoe vortex, the upstream-directed jet formed by the deflected downflow undergoes a deceleration which gives rise to a strong production of turbulent kinetic energy. We find that pressure transport of turbulent kinetic energy is important for the initiation of the large production rates by increasing the turbulence level in the upstream jet near the wall. The distribution of the dissipation of turbulent kinetic energy is similar to that of the turbulent kinetic energy. Large values of dissipation occur around the centre of the horseshoe vortex and near the wall in the region where the jet decelerates. While the small scales are nearly isotropic in the horseshoe vortex centre, they are anistotropic near the wall. This can be explained by a vertical flapping of the upstream-directed jet. The distribution and level of dissipation, turbulent and pressure transport of turbulent kinetic energy are of crucial interest to turbulence modelling in the Reynolds-averaged context. To the best of our knowledge, this is the first time that these terms have been documented in this kind of flow.
$Re_{D}=39\,000$. As the cylinder is placed in an open channel, we take special care to simulate open-channel flow as the inflow condition, including secondary flows that match the inflow in the experiment. Due to the high numerical resolution, subgrid contributions to the Reynolds stresses are negligible and the modelled dissipation plays a minor role in major parts of the flow field. The accordance of the experimental and numerical results is good. The shear in the approach flow creates a vertical pressure gradient, inducing a downflow in the cylinder front. This downflow, when deflected in the upstream direction at the bottom plate, gives rise to a so-called horseshoe vortex system. The most upstream point of flow reversal at the wall is found to be a stagnation point which appears as a sink instead of a separation point in the symmetry plane in front of the cylinder. The wall shear stress is largest between the main (horseshoe) vortex and the cylinder, and seems to be mainly governed by the strong downflow in front of the cylinder as turbulent stresses are small in this region. Due to a strong acceleration along the streamlines, a region of relatively small turbulent kinetic energy is found between the horseshoe vortex and the cylinder. When passing under the horseshoe vortex, the upstream-directed jet formed by the deflected downflow undergoes a deceleration which gives rise to a strong production of turbulent kinetic energy. We find that pressure transport of turbulent kinetic energy is important for the initiation of the large production rates by increasing the turbulence level in the upstream jet near the wall. The distribution of the dissipation of turbulent kinetic energy is similar to that of the turbulent kinetic energy. Large values of dissipation occur around the centre of the horseshoe vortex and near the wall in the region where the jet decelerates. While the small scales are nearly isotropic in the horseshoe vortex centre, they are anistotropic near the wall. This can be explained by a vertical flapping of the upstream-directed jet. The distribution and level of dissipation, turbulent and pressure transport of turbulent kinetic energy are of crucial interest to turbulence modelling in the Reynolds-averaged context. To the best of our knowledge, this is the first time that these terms have been documented in this kind of flow.
Please note a has been issued for this article.