Article contents
A tale of two airfoils: resolvent-based modelling of an oscillator versus an amplifier from an experimental mean
Published online by Cambridge University Press: 24 October 2019
Abstract
The flows around a NACA 0018 airfoil at a chord-based Reynolds number of 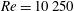 $Re=10\,250$ and angles of attack of
$Re=10\,250$ and angles of attack of 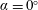 $\unicode[STIX]{x1D6FC}=0^{\circ }$ and
$\unicode[STIX]{x1D6FC}=0^{\circ }$ and 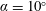 $\unicode[STIX]{x1D6FC}=10^{\circ }$ are modelled using resolvent analysis and limited experimental measurements obtained from particle image velocimetry. The experimental mean velocity fields are data assimilated so that they are solutions of the incompressible Reynolds-averaged Navier–Stokes equations forced by Reynolds stress terms which are derived from experimental data. Resolvent analysis of the data-assimilated mean velocity fields reveals low-rank behaviour only in the vicinity of the shedding frequency for
$\unicode[STIX]{x1D6FC}=10^{\circ }$ are modelled using resolvent analysis and limited experimental measurements obtained from particle image velocimetry. The experimental mean velocity fields are data assimilated so that they are solutions of the incompressible Reynolds-averaged Navier–Stokes equations forced by Reynolds stress terms which are derived from experimental data. Resolvent analysis of the data-assimilated mean velocity fields reveals low-rank behaviour only in the vicinity of the shedding frequency for 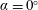 $\unicode[STIX]{x1D6FC}=0^{\circ }$ and none of its harmonics. The resolvent operator for the
$\unicode[STIX]{x1D6FC}=0^{\circ }$ and none of its harmonics. The resolvent operator for the 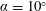 $\unicode[STIX]{x1D6FC}=10^{\circ }$ case, on the other hand, identifies two linear mechanisms whose frequencies are a close match with those identified by spectral proper orthogonal decomposition. It is also shown that the second linear mechanism, corresponding to the Kelvin–Helmholtz instability in the shear layer, cannot be identified just by considering the time-averaged experimental measurements as an input for resolvent analysis due to missing data near the leading edge. For both cases, resolvent modes resemble those from spectral proper orthogonal decomposition when the resolvent operator is low rank. The
$\unicode[STIX]{x1D6FC}=10^{\circ }$ case, on the other hand, identifies two linear mechanisms whose frequencies are a close match with those identified by spectral proper orthogonal decomposition. It is also shown that the second linear mechanism, corresponding to the Kelvin–Helmholtz instability in the shear layer, cannot be identified just by considering the time-averaged experimental measurements as an input for resolvent analysis due to missing data near the leading edge. For both cases, resolvent modes resemble those from spectral proper orthogonal decomposition when the resolvent operator is low rank. The 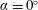 $\unicode[STIX]{x1D6FC}=0^{\circ }$ case is classified as an oscillator and its harmonics, where the resolvent operator is not low rank, are modelled using parasitic modes as opposed to classical resolvent modes which are the most amplified. The
$\unicode[STIX]{x1D6FC}=0^{\circ }$ case is classified as an oscillator and its harmonics, where the resolvent operator is not low rank, are modelled using parasitic modes as opposed to classical resolvent modes which are the most amplified. The 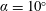 $\unicode[STIX]{x1D6FC}=10^{\circ }$ case behaves more like an amplifier and its nonlinear forcing is far less structured. The two cases suggest that resolvent-based modelling can be achieved for more complex flows with limited experimental measurements.
$\unicode[STIX]{x1D6FC}=10^{\circ }$ case behaves more like an amplifier and its nonlinear forcing is far less structured. The two cases suggest that resolvent-based modelling can be achieved for more complex flows with limited experimental measurements.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
Symon et al. supplementary movie 1
Reduced-order model for the A0 case containing 91 resolvent modes.
Symon et al. supplementary movie 2
Filtered PIV for the A0 case containing the same frequencies as the resolvent model.
- 34
- Cited by


