Article contents
Three-dimensional stability analysis for a salt-finger convecting layer
Published online by Cambridge University Press: 26 February 2018
Abstract
A three-dimensional linear stability analysis is carried out for a convecting layer in which both the temperature and solute distributions are linear in the horizontal direction. The three-dimensional results show that, for 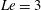 $Le=3$ and 100, the most unstable mode occurs invariably as the longitudinal mode, a vortex roll with its axis perpendicular to the longitudinal plane, suggesting that the two-dimensional results are sufficient to illustrate the stability characteristics of the convecting layer. Two-dimensional results show that the stability boundaries of the transverse mode (a vortex roll with its axis perpendicular to the transverse plane) and the longitudinal modes are virtually overlapped in the regime dominated by thermal diffusion and the regime dominated by solute diffusion, while these two modes hold a significant difference in the regime the salt-finger instability prevails. More precisely, the instability area in terms of thermal Grashof number
$Le=3$ and 100, the most unstable mode occurs invariably as the longitudinal mode, a vortex roll with its axis perpendicular to the longitudinal plane, suggesting that the two-dimensional results are sufficient to illustrate the stability characteristics of the convecting layer. Two-dimensional results show that the stability boundaries of the transverse mode (a vortex roll with its axis perpendicular to the transverse plane) and the longitudinal modes are virtually overlapped in the regime dominated by thermal diffusion and the regime dominated by solute diffusion, while these two modes hold a significant difference in the regime the salt-finger instability prevails. More precisely, the instability area in terms of thermal Grashof number 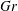 $Gr$ and solute Grashof number
$Gr$ and solute Grashof number 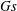 $Gs$ is larger for the longitudinal mode than the transverse mode, implying that, under any circumstance, the longitudinal mode is always more unstable than the transverse mode.
$Gs$ is larger for the longitudinal mode than the transverse mode, implying that, under any circumstance, the longitudinal mode is always more unstable than the transverse mode.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 12
- Cited by


