Published online by Cambridge University Press: 09 June 2014
The excursion number, 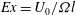 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Ex = U_0/\varOmega l$, is a parameter that characterizes the ratio of streamwise fluid advection during a tidal oscillation of amplitude
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}Ex = U_0/\varOmega l$, is a parameter that characterizes the ratio of streamwise fluid advection during a tidal oscillation of amplitude 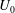 $U_0$ and frequency
$U_0$ and frequency 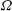 $\varOmega $ to the streamwise topographic length scale
$\varOmega $ to the streamwise topographic length scale 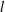 $l$. Direct numerical simulations are performed to study how internal gravity waves and turbulence change when
$l$. Direct numerical simulations are performed to study how internal gravity waves and turbulence change when 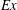 $Ex$ is varied from a low value (typical of a ridge in the deep ocean) to a value of unity (corresponding to energetic tides over a small topographic feature). An isolated obstacle having a smoothed triangular shape and 20 % of the streamwise length at critical slope is considered. With increasing values of
$Ex$ is varied from a low value (typical of a ridge in the deep ocean) to a value of unity (corresponding to energetic tides over a small topographic feature). An isolated obstacle having a smoothed triangular shape and 20 % of the streamwise length at critical slope is considered. With increasing values of 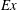 $Ex$, the near field of the internal waves loses its beam-like character, the wave response becomes asymmetric with respect to the ridge centre, and transient lee waves form. Analysis of the baroclinic energy balance shows significant reduction in the radiated wave flux in the cases with higher
$Ex$, the near field of the internal waves loses its beam-like character, the wave response becomes asymmetric with respect to the ridge centre, and transient lee waves form. Analysis of the baroclinic energy balance shows significant reduction in the radiated wave flux in the cases with higher 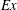 $Ex$ owing to a substantial rise in advection and baroclinic dissipation as well as a decrease in conversion. Turbulence changes qualitatively with increasing
$Ex$ owing to a substantial rise in advection and baroclinic dissipation as well as a decrease in conversion. Turbulence changes qualitatively with increasing 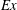 $Ex$. In the situation with
$Ex$. In the situation with 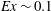 $Ex \sim 0.1$, turbulence is intensified at the near-critical regions of the slope, and is also significant in the internal wave beams above the ridge where there is intensified shear. At
$Ex \sim 0.1$, turbulence is intensified at the near-critical regions of the slope, and is also significant in the internal wave beams above the ridge where there is intensified shear. At 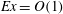 $Ex = O(1)$, the transient lee waves overturn adjacent to the ridge flanks and, owing to convective instability, buoyancy acts as a source for turbulent kinetic energy. The size of the turbulent overturns has a non-monotonic dependence on excursion number: the largest overturns, as tall as twice the obstacle height, occur in the
$Ex = O(1)$, the transient lee waves overturn adjacent to the ridge flanks and, owing to convective instability, buoyancy acts as a source for turbulent kinetic energy. The size of the turbulent overturns has a non-monotonic dependence on excursion number: the largest overturns, as tall as twice the obstacle height, occur in the 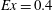 $Ex = 0.4$ case, but there is a substantial decrease of overturn size at larger values of
$Ex = 0.4$ case, but there is a substantial decrease of overturn size at larger values of 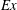 $Ex$ simulated here.
$Ex$ simulated here.