Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Berk, Tim
and
Ganapathisubramani, Bharathram
2019.
Effects of vortex-induced velocity on the development of a synthetic jet issuing into a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
651.
Asztalos, Katherine J.
Dawson, Scott T.
and
Williams, David R.
2020.
The Sensitivity of Leading-Edge Momentum Injection Response to Instantaneous Flow State for an Airfoil in Deep Stall.
Belanger, Randy
Zingg, David W.
and
Lavoie, Philippe
2020.
Vortex Structure of a Synthetic Jet Issuing into a Turbulent Boundary Layer from a Finite-span Rectangular Orifice.
Palumbo, Andrea
Semeraro, Onofrio
Robinet, Jean-Christophe
and
de Luca, Luigi
2020.
Receptivity to synthetic jet actuation in boundary layer flows.
Jankee, Girish K.
and
Ganapathisubramani, Bharathram
2021.
Scalings for rectangular synthetic jet trajectory in a turbulent boundary layer.
Journal of Fluid Mechanics,
Vol. 915,
Issue. ,
Zhao, Zhou
Ding, Junfei
Shi, Shengxian
Kaufmann, Rene
and
Ganapathisubramani, Bharathram
2021.
Volumetric flow characterisation of a rectangular orifice impinging synthetic jet with single-camera light-field PIV.
Experimental Thermal and Fluid Science,
Vol. 123,
Issue. ,
p.
110327.
Asztalos, Katherine J.
Dawson, Scott T. M.
and
Williams, David R.
2021.
Modeling the Flow State Sensitivity of Actuation Response on a Stalled Airfoil.
AIAA Journal,
p.
1.
Ho, Haonan H.
Essel, Ebenezer E.
and
Sullivan, Pierre E.
2022.
The interactions of a circular synthetic jet with a turbulent crossflow.
Physics of Fluids,
Vol. 34,
Issue. 7,
Li, Biao-Hui
Wang, Kang-Jun
Wang, Yu-Fei
and
Jiang, Nan
2022.
Experimental investigation on drag reduction in a turbulent boundary layer with a submerged synthetic jet.
Chinese Physics B,
Vol. 31,
Issue. 2,
p.
024702.
Zhang, Jin-Hao
Li, Biao-Hui
Wang, Yu-Fei
and
Jiang, Nan
2022.
Effects of single synthetic jet on turbulent boundary layer.
Chinese Physics B,
Vol. 31,
Issue. 7,
p.
074702.
Tricouros, Frank A.
Amitay, Michael
and
Van Buren, Tyler
2022.
Comparing steady and unsteady rectangular jets issuing into a crossflow.
Journal of Fluid Mechanics,
Vol. 942,
Issue. ,
Palumbo, Andrea
Semeraro, Onofrio
Robinet, Jean-Christophe
and
de Luca, Luigi
2022.
Boundary layer transition induced by low-speed synthetic jets.
Physics of Fluids,
Vol. 34,
Issue. 12,
Li, Bo
Delichatsios, Michael A.
Ji, Jie
and
Simeoni, Albert
2023.
Experimental and theoretical study of combustion and aerothermodynamic effects on the flame structure from wind-driven rectangular fires.
Fire Safety Journal,
Vol. 137,
Issue. ,
p.
103734.
Zhang, Jin-hao
Li, Biao-hui
Ping, Tian-hai
and
Jiang, Nan
2023.
Effects of single circular synthetic jet on turbulent boundary layer.
Journal of Hydrodynamics,
Vol. 35,
Issue. 3,
p.
449.
Panda, Samarendra
Pasa, Jangyadatta
and
Arumuru, Venugopal
2023.
Characterisation of an independently controlled coaxial synthetic jet.
Sensors and Actuators A: Physical,
Vol. 359,
Issue. ,
p.
114469.
Zhang, Jin-hao
Shi, Li-juan
Ma, Xing-yu
Tang, Zhan-qi
Cheng, Xiao-qi
and
Jiang, Nan
2024.
Tomographic particle image velocimetry measurements of synthetic jet in turbulent boundary layer.
Journal of Hydrodynamics,
Vol. 36,
Issue. 5,
p.
854.
Jankee, Girish K.
Yadala, Srikar
Æsøy, Eirik
Dawson, James R.
and
Worth, Nicholas A.
2025.
Scaling and dynamics of vortex lock-in for circular cylinders in an oscillating flow.
Journal of Fluid Mechanics,
Vol. 1002,
Issue. ,
Kara, Emre
2025.
Parametric Analysis and Design Optimization of a Loudspeaker-Driven Synthetic Jet Actuator Using Response Surface Model in Quiescent Conditions.
International Journal of Computational Methods,
Vol. 22,
Issue. 05,
Cruikshank, Ross
Baba, Satoshi
and
Lavoie, Philippe
2025.
The relationship between induced three-dimensional vortical structures in the wake and the drag of a profiled blunt trailing edge body.
Journal of Fluid Mechanics,
Vol. 1008,
Issue. ,
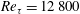 $Re_{\unicode[STIX]{x1D70F}}=12\,800$) of the cross-flow. To our knowledge, this is the first study to investigate the effect of the friction Reynolds number of the cross-flow on the trajectory of an (unsteady) jet, as well as the first study to systematically investigate the scaling of the trajectory with actuation frequency. A broad range of parameters is varied (rather than an in-depth investigation of a single parameter) and the results of this study are meant to indicate the relative importance of each parameter rather than the exact influence on the trajectory. Within the range of parameters explored, the critical ones are found to be the velocity ratio as well as a non-dimensional frequency based on the jet actuation frequency, the cross-flow velocity and the jet dimensions. The Reynolds number of the boundary layer is shown to have only a small effect on the trajectory. An expression for the trajectory of the jet is derived from the data, which (in the limit) is consistent with known expressions for the trajectory of a steady jet in a cross-flow.
$Re_{\unicode[STIX]{x1D70F}}=12\,800$) of the cross-flow. To our knowledge, this is the first study to investigate the effect of the friction Reynolds number of the cross-flow on the trajectory of an (unsteady) jet, as well as the first study to systematically investigate the scaling of the trajectory with actuation frequency. A broad range of parameters is varied (rather than an in-depth investigation of a single parameter) and the results of this study are meant to indicate the relative importance of each parameter rather than the exact influence on the trajectory. Within the range of parameters explored, the critical ones are found to be the velocity ratio as well as a non-dimensional frequency based on the jet actuation frequency, the cross-flow velocity and the jet dimensions. The Reynolds number of the boundary layer is shown to have only a small effect on the trajectory. An expression for the trajectory of the jet is derived from the data, which (in the limit) is consistent with known expressions for the trajectory of a steady jet in a cross-flow.

