Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-15T01:41:20.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitional structures in annular Poiseuille flow depending on radius ratio

Published online by Cambridge University Press:  05 April 2016

Takahiro Ishida ,
Yohann Duguet  and
Takahiro Tsukahara
Takahiro Ishida*
Affiliation:
Department of Mechanical Engineering, Tokyo University of Science, Yamazaki 2641, Noda-shi, Chiba 278-8510, Japan
Yohann Duguet
Affiliation:
LIMSI-CNRS, Université Paris-Sud, Université Paris-Saclay, F-91405 Orsay, France
Takahiro Tsukahara
Affiliation:
Department of Mechanical Engineering, Tokyo University of Science, Yamazaki 2641, Noda-shi, Chiba 278-8510, Japan
*
†Email address for correspondence: takahiro.ishida7@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

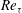The transitional regime of incompressible pressure-driven flows inside an annular pipe is investigated using accurate direct numerical simulation in long computational domains. At marginally low friction Reynolds number $Re_{{\it\tau}}$, turbulence occurs in the form of intermittent localised structures. Different types of localisation are identified as the aspect ratio is varied from 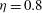${\it\eta}=0.8$ to $0.1$. These coherent structures vary from helical turbulence at 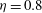${\it\eta}=0.8$ to streamwise-localised puffs at 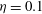${\it\eta}=0.1$. They are respectively analogous to the stripe patterns and puffs formerly identified in plane channel flow and cylindrical pipe flow. Helical turbulence has been tracked down to 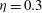${\it\eta}=0.3$, accompanied by a monotonic reduction of the pitch angle. For 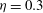${\it\eta}=0.3$ and marginally low 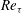$Re_{{\it\tau}}$, these turbulence structures localise in the streamwise direction, giving rise to a new regime of helical puffs with chirality. The present results suggest that helical puffs mediate the transition from globally axisymmetric puffs to helical stripe patterns.

JFM classification

Instability: Instability Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent transition
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 794 , 10 May 2016 , R2
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, H., Kawamura, H. & Matsuo, Y. 2001 Direct numerical simulation of a fully developed turbulent channel flow with respect to the Reynolds number dependence. Trans. ASME J. Fluids Engng 123 (2), 382–393.CrossRefGoogle Scholar
Avila, K., Moxey, D., de Lozar, A., Avila, M., Barkley, D. & Hof, B. 2011 The onset of turbulence in pipe flow. Science 333 (6039), 192–196.CrossRefGoogle ScholarPubMed
Avila, M. & Hof, B. 2013 Nature of laminar-turbulence intermittency in shear flows. Phys. Rev. E 87 (6), 063012.CrossRefGoogle ScholarPubMed
Barkley, D. 2011 Simplifying the complexity of pipe flow. Phys. Rev. E 84 (1), 016309.CrossRefGoogle ScholarPubMed
Chung, S.-Y., Rhee, G.-H. & Sung, H.-J. 2002 Direct numerical simulation of turbulent concentric annular pipe flow: Part 1: flow field. Intl J. Heat Fluid Flow 23 (4), 426–440.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (03), 385–425.CrossRefGoogle Scholar
Cotrell, D. L. & Pearlstein, A. J. 2006 Linear stability of spiral and annular Poiseuille flow for small radius ratio. J. Fluid Mech. 547, 1–20.CrossRefGoogle Scholar
Duguet, Y. & Schlatter, P. 2013 Oblique laminar–turbulent interfaces in plane shear flows. Phys. Rev. Lett. 110 (3), 034502.CrossRefGoogle ScholarPubMed
Duguet, Y., Schlatter, P. & Henningson, D. S. 2010 Formation of turbulent patterns near the onset of transition in plane Couette flow. J. Fluid Mech. 650, 119–129.CrossRefGoogle Scholar
Heaton, C. J. 2008 Linear instability of annular Poiseuille flow. J. Fluid Mech. 610, 391–406.CrossRefGoogle Scholar
Lemoult, G., Shi, L., Avila, K., Jalikop, S., Avila, M. & Hof, B. 2016 Directed percolation phase transition to sustained turbulence in Couette flow. Nature Phys 12, 254–258.CrossRefGoogle Scholar
Manneville, P. 2015 On the transition to turbulence of wall-bounded flows in general, and plane Couette flow in particular. Eur. J. Phys. B 49, 345–362.Google Scholar
Moin, P. & Kim, J. 1982 Numerical investigation of turbulent channel flow. J. Fluid Mech. 118, 341–377.CrossRefGoogle Scholar
Mott, J. E. & Joseph, D. D. 1968 Stability of parallel flow between concentric cylinders. Phys. Fluids 11 (10), 2065–2073.CrossRefGoogle Scholar
Moxey, D. & Barkley, D. 2010 Distinct large-scale turbulent-laminar states in transitional pipe flow. Proc. Natl Acad. Sci. USA 107 (18), 8091–8096.CrossRefGoogle ScholarPubMed
Prigent, A., Grégoire, G., Chaté, H., Dauchot, O. & van Saarloos, W. 2002 Large-scale finite-wavelength modulation within turbulent shear flows. Phys. Rev. Lett. 89 (1), 014501.CrossRefGoogle ScholarPubMed
Rodriguez-Corredor, F. E., Bizhani, M., Ashrafuzzaman, M. & Kuru, E. 2014 An experimental investigation of turbulent water flow in concentric annulus using particle image velocimetry technique. Trans. ASME J. Fluids Engng 136 (5), 051203.CrossRefGoogle Scholar
Samanta, D., de Lozar, A. & Hof, B. 2011 Experimental investigation of laminar turbulent intermittency in pipe flow. J. Fluid Mech. 681, 193–204.CrossRefGoogle Scholar
Sano, M. & Tamai, K. 2016 A universal transition to turbulence in channel flow. Nature Phys. 12, 249–253.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Shi, L., Avila, M. & Hof, B. 2013 Scale invariance at the onset of turbulence in Couette flow. Phys. Rev. Lett. 110 (20), 204502.CrossRefGoogle ScholarPubMed
Shimizu, M., Manneville, P., Duguet, Y. & Kawahara, G. 2014 Splitting of a turbulent puff in pipe flow. Fluid Dyn. Res. 46 (6), 061403.CrossRefGoogle Scholar
Tsukahara, T., Kawaguchi, Y., Kawamura, H., Tillmark, N. & Alfredsson, P. H. 2010 Turbulence stripe in transitional channel flow with/without system rotation. In Proceedings of the Seventh IUTAM Symp. on Laminar-Turbulent Transition (ed. Schlatter, P. & Henningson, D. S.), pp. 421–426. Springer.CrossRefGoogle Scholar
Tsukahara, T., Seki, Y., Kawamura, H. & Tochio, D. 2005 DNS of turbulent channel flow at very low Reynolds numbers. In Proceedings of the Fourth International Symp. on Turbulence and Shear Flow Phenomena, Williamsburg, USA (ed. Humphrey, J. A. C. et al. ), pp. 935–940. arXiv:1406.0248.CrossRefGoogle Scholar
Tuckerman, L. S., Kreilos, T., Schrobsdorff, H., Schneider, T. M. & Gibson, J. F. 2014 Turbulent-laminar patterns in plane Poiseuille flow. Phys. Fluids 26, 114103.CrossRefGoogle Scholar
Walker, J. E., Whan, G. A. & Rothfus, R. R. 1957 Fluid friction in noncircular ducts. AIChE J. 3 (4), 484–489.CrossRefGoogle Scholar
Wygnanski, I. J. & Champagne, F. H. 1973 On transition in a pipe. Part 1. The origin of puffs and slugs and the flow in a turbulent slug. J. Fluid Mech. 59 (2), 281–335.CrossRefGoogle Scholar
Xiong, X., Tao, J., Chen, S. & Brandt, L. 2015 Turbulent bands in plane-Poiseuille flow at moderate Reynolds numbers. Phys. Fluids 27, 041702.CrossRefGoogle Scholar