Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gevorkyan, L.
Shoji, T.
Peng, W. Y.
and
Karagozian, A. R.
2018.
Influence of the velocity field on scalar transport in gaseous transverse jets.
Journal of Fluid Mechanics,
Vol. 834,
Issue. ,
p.
173.
Miller, Warrick A.
Medwell, Paul R.
Doolan, Con J.
and
Kim, Minkwan
2018.
Transient interaction between a reaction control jet and a hypersonic crossflow.
Physics of Fluids,
Vol. 30,
Issue. 4,
Miller, Warrick A.
Medwell, Paul R.
Doolan, Con J.
and
Kim, Minkwan
2018.
Numerical investigation of a pulsed reaction control jet in hypersonic crossflow.
Physics of Fluids,
Vol. 30,
Issue. 10,
Connor, Erin G.
McHugh, Margaret K.
and
Crimaldi, John P.
2018.
Quantification of airborne odor plumes using planar laser-induced fluorescence.
Experiments in Fluids,
Vol. 59,
Issue. 9,
Dayton, James W.
Poettgen, Benjamin K.
Linevitch, Kyle
and
Cetegen, Baki M.
2019.
Non-isothermal mixing characteristics in the extreme near-field of a turbulent jet in hot crossflow.
Physics of Fluids,
Vol. 31,
Issue. 12,
Shoji, Takeshi
Besnard, Andrea
Harris, Elijah W.
M’Closkey, Robert T.
and
Karagozian, Ann R.
2019.
Effects of Axisymmetric Square-Wave Excitation on Transverse Jet Structure and Mixing.
AIAA Journal,
Vol. 57,
Issue. 5,
p.
1862.
Besnard, Andrea
Shoji, Takeshi
Schein, Stephen
Harris, Elijah
and
Karagozian, Ann R.
2019.
Exploration of Asymmetric Forcing on Mixing and Structural Characteristics for Transverse Jets.
Nair, Vedanth
Sirignano, Matthew
Emerson, Benjamin
Halls, Ben
Jiang, Naibo
Felver, Josef
Roy, Sukesh
Gord, Jim
and
Lieuwen, Tim
2019.
Counter rotating vortex pair structure in a reacting jet in crossflow.
Proceedings of the Combustion Institute,
Vol. 37,
Issue. 2,
p.
1489.
Kok, Besir
2020.
Thermo-hydraulic properties of a transverse-jet in a crossflow channel using nanofluids.
Progress in Nuclear Energy,
Vol. 123,
Issue. ,
p.
103305.
Dayton, James W.
Poettgen, Benjamin K.
and
Cetegen, Baki M.
2020.
Non-isothermal mixing characteristics in the extreme near-field of turbulent jets in hot crossflow: Effects of jet exit turbulence and velocity profile.
Physics of Fluids,
Vol. 32,
Issue. 11,
Shoji, Takeshi
Harris, Elijah W.
Besnard, Andrea
and
Karagozian, Ann R.
2020.
Effects of Sinusoidal Excitation on Transverse Jet Dynamics, Structure, and Mixing.
AIAA Journal,
Vol. 58,
Issue. 9,
p.
3889.
Getsinger, D. R.
Gevorkyan, L.
Shoji, T.
Smith, O. I.
and
Karagozian, A. R.
2020.
Structural and stability characteristics of jets in crossflow – CORRIGENDUM.
Journal of Fluid Mechanics,
Vol. 890,
Issue. ,
Nair, Vedanth
Sirignano, Matthew D.
Schmidheiser, Sara
Dillon, Lane
Fugger, Christopher A.
Yi, Tongxun
Jiang, Naibo
Hsu, Paul S.
Slipchenko, Mikhail N.
Roy, Sukesh
Emerson, Benjamin L.
Steinberg, Adam M.
and
Lieuwen, Tim C.
2020.
Tomographic PIV Characterization of the Near field Topology of the Reacting Jet in Crossflow.
Shoji, Takeshi
Harris, Elijah W.
Besnard, Andrea
Schein, Stephen G.
and
Karagozian, Ann R.
2020.
Transverse jet lock-in and quasiperiodicity.
Physical Review Fluids,
Vol. 5,
Issue. 1,
Fedorova, N N
Goldfeld, M A
and
Valger, S A
2020.
Influence of the relative momentum flux ratio on the mixing of hydrogen jets in an M=4 crossflow.
Journal of Physics: Conference Series,
Vol. 1677,
Issue. 1,
p.
012039.
Liu, Enhui
Liu, Xiao
Zhao, Majie
Zheng, Hongtao
Lu, Jinghe
and
Zhang, Zhihao
2020.
Turbulent fuel-air mixing study of jet in crossflow at different velocity ratios using LES.
International Journal of Heat and Fluid Flow,
Vol. 85,
Issue. ,
p.
108633.
Sirignano, M. D.
Nair, V.
Emerson, B. L.
Seitzman, J.
and
Lieuwen, T. C.
2020.
Nitrogen Oxide Emissions from Premixed Reacting Jets in a Vitiated Crossflow.
Combustion Science and Technology,
Vol. 192,
Issue. 7,
p.
1389.
Shoji, Takeshi
Harris, Elijah W.
Besnard, Andrea
Schein, Stephen G.
and
Karagozian, Ann R.
2020.
On the origins of transverse jet shear layer instability transition.
Journal of Fluid Mechanics,
Vol. 890,
Issue. ,
Li, Jin-ping
Chen, Shu-sheng
Cai, Fang-jie
and
Yan, Chao
2020.
Numerical investigation of vented plume into a supersonic flow in the early stage of rocket hot separation.
Aerospace Science and Technology,
Vol. 107,
Issue. ,
p.
106249.
Fries, Dan
Ranjan, Devesh
and
Menon, Suresh
2021.
Turbulent mixing and trajectories of jets in a supersonic cross-flow with different injectants.
Journal of Fluid Mechanics,
Vol. 911,
Issue. ,
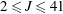 $2\leqslant J\leqslant 41$), density ratios (
$2\leqslant J\leqslant 41$), density ratios ( $0.35\leqslant S\leqslant 1.0$) and injector configurations (flush nozzle, flush pipe and elevated nozzle), all at a fixed jet Reynolds number of 1900. For the majority of conditions explored, there is a direct correspondence between the nature of the jet’s upstream shear layer instabilities and structure, as documented in detail in Getsinger et al. (J. Fluid Mech., vol. 760, 2014, pp. 342–367), and the jet’s mixing characteristics, consistent with diffusion-dominated processes, but with a few notable exceptions. When quantified as a function of distance along the jet trajectory, mixing metrics for jets in cross-flow with an absolutely unstable upstream shear layer and relatively symmetric counter-rotating vortex pair cross-sectional structure tend to show better local molecular mixing than for jets with convectively unstable upstream shear layers and generally asymmetric cross-sectional structures. Yet the spatial evolution of mixing with downstream distance can be greater for a few specific convectively unstable conditions, apparently associated with the initiation and nature of shear layer rollup as a trigger for improved mixing. A notable exception to these trends concerns conditions where the equidensity jet in cross-flow has an upstream shear layer that is already absolutely unstable, and the jet density is then reduced in comparison with that of the cross-flow. Here, density ratios below unity tend to mix less well than for equidensity conditions, demonstrated to result from differences in the nature of higher-density cross-flow entrainment into lower-density shear layer vortices.
$0.35\leqslant S\leqslant 1.0$) and injector configurations (flush nozzle, flush pipe and elevated nozzle), all at a fixed jet Reynolds number of 1900. For the majority of conditions explored, there is a direct correspondence between the nature of the jet’s upstream shear layer instabilities and structure, as documented in detail in Getsinger et al. (J. Fluid Mech., vol. 760, 2014, pp. 342–367), and the jet’s mixing characteristics, consistent with diffusion-dominated processes, but with a few notable exceptions. When quantified as a function of distance along the jet trajectory, mixing metrics for jets in cross-flow with an absolutely unstable upstream shear layer and relatively symmetric counter-rotating vortex pair cross-sectional structure tend to show better local molecular mixing than for jets with convectively unstable upstream shear layers and generally asymmetric cross-sectional structures. Yet the spatial evolution of mixing with downstream distance can be greater for a few specific convectively unstable conditions, apparently associated with the initiation and nature of shear layer rollup as a trigger for improved mixing. A notable exception to these trends concerns conditions where the equidensity jet in cross-flow has an upstream shear layer that is already absolutely unstable, and the jet density is then reduced in comparison with that of the cross-flow. Here, density ratios below unity tend to mix less well than for equidensity conditions, demonstrated to result from differences in the nature of higher-density cross-flow entrainment into lower-density shear layer vortices.