Article contents
Travelling waves in elliptic pipe flow
Published online by Cambridge University Press: 22 July 2021
Abstract
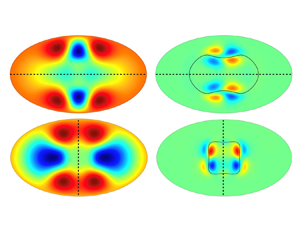
Families of exact coherent states in elliptical pipe flow obtained from the travelling-wave solutions in circular pipe flow by a continuation approach are found. Results are given in a regime of the aspect ratio  $A$ in which the laminar flow is linearly stable. The results suggest the possibility of two distinct classes of solutions of elliptical travelling waves at higher values of
$A$ in which the laminar flow is linearly stable. The results suggest the possibility of two distinct classes of solutions of elliptical travelling waves at higher values of  $A$: (i) rotationally symmetric centre-mode states that collapse towards the pipe centre and (ii) rotationally asymmetric vortex–wave interaction states with additional mirror symmetry exhibiting organization of the waves around a critical layer. These are the first calculations of three-dimensional travelling waves in elliptical pipes. Investigation of these states has the potential to provide fresh insight into the relationship between exact coherent structures in Poiseuille flow in pipes and channels.
$A$: (i) rotationally symmetric centre-mode states that collapse towards the pipe centre and (ii) rotationally asymmetric vortex–wave interaction states with additional mirror symmetry exhibiting organization of the waves around a critical layer. These are the first calculations of three-dimensional travelling waves in elliptical pipes. Investigation of these states has the potential to provide fresh insight into the relationship between exact coherent structures in Poiseuille flow in pipes and channels.
JFM classification
Information
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 2
- Cited by


