Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-11T03:56:39.479Z Has data issue: false hasContentIssue false
  • English
  • Français

The turbulence boundary of a temporal jet

Published online by Cambridge University Press:  18 December 2013

Maarten van Reeuwijk  and
Markus Holzner
Maarten van Reeuwijk*
Affiliation:
Department of Civil and Environmental Engineering, Imperial College London, SW7 2AZ London, UK
Markus Holzner
Affiliation:
Institute of Environmental Engineering, ETH Zürich, CH-8039 Zürich, Switzerland
*
†Email address for correspondence: m.vanreeuwijk@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the structure of the turbulence boundary of a temporal plane jet at 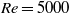$\mathit{Re}= 5000$ using statistics conditioned on the enstrophy. The data is obtained by direct numerical simulation and threshold values span 24 orders of magnitude, ranging from essentially irrotational fluid outside the jet to fully turbulent fluid in the jet core. We use two independent estimators for the local entrainment velocity 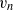${v}_{n} $ based on the enstrophy budget. The data show clear evidence for the existence of a viscous superlayer (VSL) that envelopes the turbulence. The VSL is a nearly one-dimensional layer with low surface curvature. We find that both its area and viscous transport velocity adjust to the imposed rate of entrainment so that the integral entrainment flux is independent of threshold, although low-Reynolds-number effects play a role for the case under consideration. This threshold independence is consistent with the inviscid nature of the integral rate of entrainment. A theoretical model of the VSL is developed that is in reasonably good agreement with the data and predicts that the contribution of viscous transport and dissipation to interface propagation have magnitude 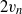$2{v}_{n} $ and 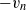$- {v}_{n} $, respectively. We further identify a turbulent core region (TC) and a buffer region (BR) connecting the VSL and the TC. The BR grows in time and inviscid enstrophy production is important in this region. The BR shows many similarities with the turbulent–non-turbulent interface (TNTI), although the TNTI seems to extend into the TC. The average distance between the TC and the VSL, i.e. the BR thickness is about 10 Kolmogorov length scales or half a Taylor length scale, indicating that intense turbulent flow regions and viscosity-dominated regions are in close proximity.

JFM classification

Wakes/Jets: Wakes/Jets Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 739 , 25 January 2014 , pp. 254 - 275
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A. L. 1955 Free stream boundaries of turbulent flows. Tech. Rep. 1244. NACA.Google Scholar
Da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2013 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 457–490.Google Scholar
Da Silva, C. B. & Métais, O. 2002 On the influence of coherent structures upon interscale interactions in turbulent plane jets. J. Fluid Mech. 473, 103–145.CrossRefGoogle Scholar
Da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/non-turbulent interface in jets. Phys. Fluids 20 (5), 055101.Google Scholar
Da Silva, C. B. & Taveira, R. P. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22 (5), 121702.Google Scholar
Gutmark, E. & Wygnansky, I. 1976 The planar turbulent jet. J. Fluid Mech. 73, 465–495.CrossRefGoogle Scholar
Holzner, M., Liberzon, A., Nikitin, N., Kinzelbach, W. & Tsinober, A. 2007 Small-scale aspects of flows in proximity of the turbulent/nonturbulent interface. Phys. Fluids 19 (7), 071702.Google Scholar
Holzner, M., Liberzon, A., Nikitin, N., Luethi, B., Kinzelbach, W. & Tsinober, A. 2008 A Lagrangian investigation of the small-scale features of turbulent entrainment through particle tracking and direct numerical simulation. J. Fluid Mech. 598, 465–475.Google Scholar
Holzner, M. & Luethi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Hunt, J. C. R., Eames, I., Da Silva, C. B. & Westerweel, J. 2011 Interfaces and inhomogeneous turbulence. Phil. Trans. R. Soc. A 369, 811–832.Google Scholar
Hunt, J. C. R., Eames, I. & Westerweel, J. 2008 Vortical interactions with interfacial shear layers. In IUTAM Symposium on Computational Physics and New Perspectives in Turbulence, IUTAM Bookseries, vol. 4, pp. 331–338.Google Scholar
Hunt, J. C. R., Rottman, J. W. & Britter, R. E. 1983 Some physical processes involved in the dispersion of dense gases. In Proc. UITAM Symp. on Atmospheric Dispersion of Heavy Gases and Small Particles (ed. Ooms, G. & Tennekes, H.), pp. 361–395. Springer.Google Scholar
Hyman, J. M. & Shashkov, M. 1997 Natural discretizations for the divergence, gradient, and curl on logically rectangular grids. Comput. Math. Appl. 33, 81–104.CrossRefGoogle Scholar
Mathew, J. & Basu, A. J. 2002 Some characterstics of entrainment at a cylindrical turbulence boundary. Phys. Fluids 14, 2065–2072.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitional convection from maintained and instantaneous sources. Proc. R. Soc. Lond. 234, 1–23.Google Scholar
Philip, J. & Marusic, I. 2012 Large-scale eddies and their role in entrainment in turbulent jets and wakes. Phys. Fluids 24, 055108.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Ramparian, R. & Chandrasekhara, M. S. 1985 LDA measurements in plane turbulent jets. ASME J. Fluids Engng 107, 264–271.CrossRefGoogle Scholar
Redford, J. A., Castro, I. P. & Coleman, G. N. 2012 On the universality of turbulent axisymmetric wakes. J. Fluid Mech. 710, 419–452.CrossRefGoogle Scholar
van Reeuwijk, M. 2011 A mimetic mass, momentum and energy conserving discretization for the shallow water equations. Comput. Fluids 46, 411–416.CrossRefGoogle Scholar
van Reeuwijk, M., Jonker, H. J. J. & Hanjalić, K. 2008 Wind and boundary layers in Rayleigh–Bénard convection. I. Analysis and modelling. Phys. Rev. E 77, 036311.Google Scholar
Sreenivasan, K. R. 1991 Fractals and multifractals in turbulence. Annu. Rev. Fluid Mech. 23, 539–600.CrossRefGoogle Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Stull, 1998 An Introduction to Boundary Layer Meteorology. Kluwer Academic.Google Scholar
Taveira, R. P. & Da Silva, C. B. 2013 Kinetic energy budgets near the turbulent/nonturbulent interface in jets. Phys. Fluids 25, 015114.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thorpe, S. A. 2005 The Turbulent Ocean. Cambridge University Press.CrossRefGoogle Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Tritton, D. J. 1988 Physical Fluid Dynamics. Calendon.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Verstappen, R. W. C. P. & Veldman, A. E. P. 2003 Symmetry-preserving discretization of turbulent flow. J. Comput. Phys. 187 (1), 343–368.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent–nonturbulent interface of a jet. Phys. Rev. Lett. 95 (17), 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar
Wolf, M., Lüthi, B., Holzner, M., Krug, D., Kinzelbach, W. & Tsinober, A. 2012 Investigations on the local entrainment velocity in a turbulent jet. Phys. Fluids 24 (10), 105110Attached publisher’s note: Erratum: ‘Investigations on the local entrainment velocity in a turbulent jet’ [Phys. Fluids 24, 105110 (2012)], Phys. Fluids 25, 019901 (2013).Google Scholar