Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-25T17:11:57.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulence dynamics near a turbulent/non-turbulent interface

Published online by Cambridge University Press:  13 February 2012

M. A. C. Teixeira  and
C. B. da Silva
M. A. C. Teixeira*
Affiliation:
CGUL, IDL, University of Lisbon, Edifício C8, Campo Grande, 1749-016 Lisbon, Portugal
C. B. da Silva
Affiliation:
IDMEC, IST, Technical University of Lisbon, Pav. Mecânica I, 1° andar/esq./LASEF, Av. Rovisco Pais, 1049-001 Lisbon, Portugal
*
†Email address for correspondence: mateixeira@fc.ul.pt
Get access Rights & Permissions [Opens in a new window]

Abstract

The characteristics of the boundary layer separating a turbulence region from an irrotational (or non-turbulent) flow region are investigated using rapid distortion theory (RDT). The turbulence region is approximated as homogeneous and isotropic far away from the bounding turbulent/non-turbulent (T/NT) interface, which is assumed to remain approximately flat. Inviscid effects resulting from the continuity of the normal velocity and pressure at the interface, in addition to viscous effects resulting from the continuity of the tangential velocity and shear stress, are taken into account by considering a sudden insertion of the T/NT interface, in the absence of mean shear. Profiles of the velocity variances, turbulent kinetic energy (TKE), viscous dissipation rate (), turbulence length scales, and pressure statistics are derived, showing an excellent agreement with results from direct numerical simulations (DNS). Interestingly, the normalized inviscid flow statistics at the T/NT interface do not depend on the form of the assumed TKE spectrum. Outside the turbulent region, where the flow is irrotational (except inside a thin viscous boundary layer), decays as 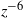, where is the distance from the T/NT interface. The mean pressure distribution is calculated using RDT, and exhibits a decrease towards the turbulence region due to the associated velocity fluctuations, consistent with the generation of a mean entrainment velocity. The vorticity variance and display large maxima at the T/NT interface due to the inviscid discontinuities of the tangential velocity variances existing there, and these maxima are quantitatively related to the thickness 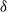of the viscous boundary layer (VBL). For an equilibrium VBL, the RDT analysis suggests that 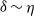(where 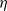is the Kolmogorov microscale), which is consistent with the scaling law identified in a very recent DNS study for shear-free T/NT interfaces.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 695 , 25 March 2012 , pp. 257 - 287
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Alvelius, K. 1999 Random forcing of three-dimensional homogeneous turbulence. Phys. Fluids 11 (7), 1880–1889.CrossRefGoogle Scholar
2. Batchelor, G. K. & Proudman, I. 1954 The effect of rapid distortion of a fluid in turbulent motion. Q. J. Mech. Appl. Maths 7, 83–103.CrossRefGoogle Scholar
3. Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
4. Burattini, P., Lavoie, P. & Antonia, R. A. 2005 On the normalized turbulent energy dissipation rate. Phys. Fluids 17, 098103.CrossRefGoogle Scholar
5. Carruthers, D. J. & Hunt, J. C. R. 1986 Velocity fluctuations near an interface between a turbulent region and a stably stratified layer. J. Fluid Mech. 165, 475–501.CrossRefGoogle Scholar
6. Corrsin, S. & Kistler, A. L. 1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-1244.Google Scholar
7. Fernando, H. J. S. & Hunt, J. C. R. 1997 Turbulence, waves and mixing at shear-free density interfaces. Part 1. A theoretical model. J. Fluid Mech. 347, 197–234.CrossRefGoogle Scholar
8. Hunt, J. C. R. 1984 Turbulence structure in thermal convection and shear-free boundary layers. J. Fluid Mech. 138, 161–184.CrossRefGoogle Scholar
9. Hunt, J. C. R., Eames, I. & Westerweel, J. 2006 Mechanics of inhomogeneous turbulence and interfacial layers. J. Fluid Mech. 554, 499–519.CrossRefGoogle Scholar
10. Hunt, J. C. R. & Graham, J. M. R. 1978 Free stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.CrossRefGoogle Scholar
11. Hunt, J. C. R., Stretch, D. D. & Belcher, S. E. 2011 Viscous coupling of shear-free turbulence across nearly flat fluit interfaces. J. Fluid Mech. 671, 96–120.CrossRefGoogle Scholar
12. Ishihara, T., Gotoh, T. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
13. Jiménez, J. & Wray, A. 1998 On the characteristics of vortex filaments in isotropic turbulence. J. Fluid Mech. 373, 255–285.CrossRefGoogle Scholar
14. Perot, B. & Moin, P. 1995 Shear-free turbulent boundary layers. Part 1. Physical insights into near-wall turbulence. J. Fluid Mech. 295, 199–227.CrossRefGoogle Scholar
15. Phillips, O. M. 1955 The irrotational motion outside a free turbulent boundary. Proc. Camb. Phil. Soc. 51, 220–229.CrossRefGoogle Scholar
16. da Silva, C. B. 2009 The behaviour of subgrid-scale models near the turbulent/nonturbulent interface in jets. Phys. Fluids 21, 081702.CrossRefGoogle Scholar
17. da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20, 055101.CrossRefGoogle Scholar
18. da Silva, C. B. & Reis, R. N. 2011 The role of coherent vortices near the turbulent/nonturbulent interface in a planar jet. Phil. Trans. R. Soc. Lond. A 369, 738–753.Google Scholar
19. da Silva, C. B. & Taveira, R. R. 2010 The thickness of the t/nt interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22, 121702.CrossRefGoogle Scholar
20. Teixeira, M. A. C. & Belcher, S. E. 2000 Dissipation of shear-free turbulence near boundaries. J. Fluid Mech. 422, 167–191.CrossRefGoogle Scholar
21. Teixeira, M. A. C. & Miranda, P. M. A. 1997 On the entrainment assumption in Schatzmann’s integral plume model. Appl. Sci. Res. 57, 15–42.CrossRefGoogle Scholar
22. Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.CrossRefGoogle Scholar
23. Tordella, D., Iovieno, M. & Bailey, P. R. 2008 Sufficient condition for Gaussian departure in turbulence. Phys. Rev. E 77, 016309.CrossRefGoogle ScholarPubMed
24. Townsend, A. A. 1966 The mechanism of entrainment in free turbulent flows. J. Fluid Mech. 26, 689–715.CrossRefGoogle Scholar
25. Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
26. Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.CrossRefGoogle Scholar
27. Wang, H. & George, W. K. 2002 The integral scale in homogeneous isotropic turbulence. J. Fluid Mech. 459, 429–443.CrossRefGoogle Scholar
28. Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent–nonturbulent interface of a jet. Phys. Rev. Lett. 95, 174501.CrossRefGoogle ScholarPubMed
29. Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.CrossRefGoogle Scholar