Article contents
Turbulent structure of high-amplitude pressure peaks within the turbulent boundary layer
Published online by Cambridge University Press: 24 October 2013
Abstract
The positive and negative high-amplitude pressure peaks (HAPP) are investigated in a turbulent boundary layer at 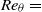 $R{e}_{\theta } = $ 1900 in order to identify their turbulent structure. The three-dimensional velocity field is measured within the inner layer of the turbulent boundary layer using tomographic particle image velocimetry (tomo-PIV). The measurements are performed at an acquisition frequency of 10 000 Hz and over a volume of
$R{e}_{\theta } = $ 1900 in order to identify their turbulent structure. The three-dimensional velocity field is measured within the inner layer of the turbulent boundary layer using tomographic particle image velocimetry (tomo-PIV). The measurements are performed at an acquisition frequency of 10 000 Hz and over a volume of 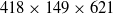 $418\times 149\times 621$ wall units in the streamwise, wall-normal and spanwise directions, respectively. The time-resolved velocity fields are applied to obtain the material derivative using the Lagrangian method followed by integration of the Poisson pressure equation to obtain the three-dimensional unsteady pressure field. The simultaneous volumetric velocity, acceleration, and pressure data are conditionally sampled based on local maxima and minima of wall pressure to analyse the three-dimensional turbulent structure of the HAPPs. Analysis has associated the positive HAPPs to the shear layer structures formed by an upstream sweep of high-speed flow opposing a downstream ejection event. The sweep event is initiated in the outer layer while the ejection of near-wall fluid is formed by the hairpin category of vortices. The shear layers were observed to be asymmetric in the instantaneous visualizations of the velocity and acceleration fields. The asymmetric pattern originates from the spanwise component of temporal acceleration of the ejection event downstream of the shear layer. The analysis also demonstrated a significant contribution of the pressure transport term to the budget of the turbulent kinetic energy in the shear layers. Investigation of the conditional averages and the orientation of the vortices showed that the negative HAPPs are linked to both the spanwise and quasi-streamwise vortices of the turbulent boundary layer. The quasi-streamwise vortices can be associated with the hairpin category of vortices or the isolated quasi-streamwise vortices of the inner layer. A bi-directional analysis of the link between the HAPPs and the hairpin paradigm is also conducted by conditionally averaging the pressure field based on the detection of hairpin vortices using strong ejection events. The results demonstrated positive pressure in the shear layer region of the hairpin model and negative pressure overlapping with the vortex core.
$418\times 149\times 621$ wall units in the streamwise, wall-normal and spanwise directions, respectively. The time-resolved velocity fields are applied to obtain the material derivative using the Lagrangian method followed by integration of the Poisson pressure equation to obtain the three-dimensional unsteady pressure field. The simultaneous volumetric velocity, acceleration, and pressure data are conditionally sampled based on local maxima and minima of wall pressure to analyse the three-dimensional turbulent structure of the HAPPs. Analysis has associated the positive HAPPs to the shear layer structures formed by an upstream sweep of high-speed flow opposing a downstream ejection event. The sweep event is initiated in the outer layer while the ejection of near-wall fluid is formed by the hairpin category of vortices. The shear layers were observed to be asymmetric in the instantaneous visualizations of the velocity and acceleration fields. The asymmetric pattern originates from the spanwise component of temporal acceleration of the ejection event downstream of the shear layer. The analysis also demonstrated a significant contribution of the pressure transport term to the budget of the turbulent kinetic energy in the shear layers. Investigation of the conditional averages and the orientation of the vortices showed that the negative HAPPs are linked to both the spanwise and quasi-streamwise vortices of the turbulent boundary layer. The quasi-streamwise vortices can be associated with the hairpin category of vortices or the isolated quasi-streamwise vortices of the inner layer. A bi-directional analysis of the link between the HAPPs and the hairpin paradigm is also conducted by conditionally averaging the pressure field based on the detection of hairpin vortices using strong ejection events. The results demonstrated positive pressure in the shear layer region of the hairpin model and negative pressure overlapping with the vortex core.
Information
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 50
- Cited by

