Article contents
Turbulent wake behind side-by-side flat plates: computational study of interference effects
Published online by Cambridge University Press: 24 September 2018
Abstract
The complex wake behind two side-by-side flat plates placed normal to the inflow direction has been explored in a direct numerical simulation study. Two gaps, 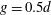 $g=0.5d$ and
$g=0.5d$ and 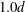 $1.0d$, were considered, both at a Reynolds number of 1000 based on the plate width
$1.0d$, were considered, both at a Reynolds number of 1000 based on the plate width 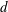 $d$ and the inflow velocity. For gap ratio
$d$ and the inflow velocity. For gap ratio 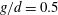 $g/d=0.5$, the biased gap flow resulted in an asymmetric flow configuration consisting of a narrow wake with strong vortex shedding and a wide wake with no periodic near-wake shedding. Shear-layer transition vortices were observed in the wide wake, with characteristic frequency 0.6. For
$g/d=0.5$, the biased gap flow resulted in an asymmetric flow configuration consisting of a narrow wake with strong vortex shedding and a wide wake with no periodic near-wake shedding. Shear-layer transition vortices were observed in the wide wake, with characteristic frequency 0.6. For 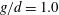 $g/d=1.0$, two simulations were performed, started from a symmetric and an asymmetric initial flow field. A symmetric configuration of Kármán vortices resulted from the first simulation. Surprisingly, however, two different three-dimensional instability features were observed simultaneously along the span of the upper and lower plates. The spanwise wavelengths of these secondary streamwise vortices, formed in the braid regions of the primary Kármán vortices, were approximately
$g/d=1.0$, two simulations were performed, started from a symmetric and an asymmetric initial flow field. A symmetric configuration of Kármán vortices resulted from the first simulation. Surprisingly, however, two different three-dimensional instability features were observed simultaneously along the span of the upper and lower plates. The spanwise wavelengths of these secondary streamwise vortices, formed in the braid regions of the primary Kármán vortices, were approximately 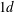 $1d$ and
$1d$ and 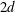 $2d$, respectively. The wake bursts into turbulence some
$2d$, respectively. The wake bursts into turbulence some 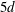 $5d$–
$5d$–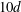 $10d$ downstream. The second simulation resulted in an asymmetric wake configuration similar to the asymmetric wake found for the narrow gap
$10d$ downstream. The second simulation resulted in an asymmetric wake configuration similar to the asymmetric wake found for the narrow gap 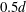 $0.5d$, with the appearance of shear-layer instabilities in the wide wake. The analogy between a plane mixing layer and the separated shear layer in the wide wake was examined. The shear-layer frequencies obtained were in close agreement with the frequency of the most amplified wave based on linear stability analysis of a plane mixing layer.
$0.5d$, with the appearance of shear-layer instabilities in the wide wake. The analogy between a plane mixing layer and the separated shear layer in the wide wake was examined. The shear-layer frequencies obtained were in close agreement with the frequency of the most amplified wave based on linear stability analysis of a plane mixing layer.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 11
- Cited by


