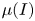 $\mu(I)$ rheology
$\mu(I)$ rheologyPublished online by Cambridge University Press: 30 April 2021
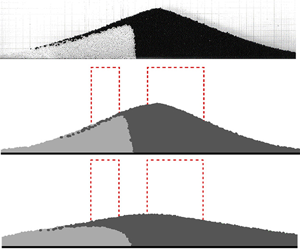
Granular column collapse involves complicated granular flow bridging initial and final solid-like states, with intermediate multi-regime spatial and temporal flow patterns and transitions, which include large free-surface variation. In this study, a non-local mesh-free numerical method is proposed to model these flows and capture the entire process from flowing to arresting. Free surface evolution is tracked by the mesh-free method while the non-local theory of peridynamics is used to capture the arresting for the flow. The constitutive relation to calculate the effective viscosity and stress is based on the μ(I) rheology. The non-local mesh-free method is validated to simulate a granular column collapse in which effects from the peridynamic horizon and particle distance are both examined. Non-local modelling is then used to simulate more types of granular column collapses, by comparison with other numerical results and experimental observations in terms of the free surface and velocity variations in both the fluid-like and solid-like states. The collision between two adjacent collapsing granular columns is also simulated, and the interface variations between material from each collapsing column are compared with experimental observations. The non-local modelling is shown to reflect the internal flow characteristics in the granular flow. Throughout these simulations, the non-local mesh-free method is able to calculate the free surface, velocity and interface variation in the granular flows.