Article contents
Velocity ratio effect on flow structures of non-parallel planar starting jets in cross-flow
Published online by Cambridge University Press: 09 March 2021
Abstract
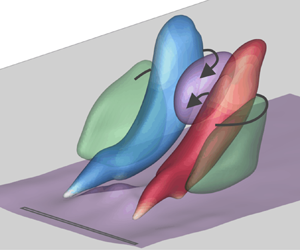
The interaction between starting jets and a steady cross-flow with a zero-pressure-gradient, turbulent boundary layer is studied experimentally. A device typically used in flow control applications is employed as jets of compressed air are injected into the cross-flow through a rectangular high-aspect-ratio outlet. Investigating different velocity ratios between starting jets and cross-flow within the interval  $r=u_{jet}/U_\infty =2.4, \ldots ,11$, we identify two regimes of different flow structure appearance, transferring the classification map applicable to parallel circular starting jets in cross-flow established by Sau & Mahesh (J. Fluid Mech., vol. 604, 2008, pp. 389–409). At
$r=u_{jet}/U_\infty =2.4, \ldots ,11$, we identify two regimes of different flow structure appearance, transferring the classification map applicable to parallel circular starting jets in cross-flow established by Sau & Mahesh (J. Fluid Mech., vol. 604, 2008, pp. 389–409). At  $r<4$, the vorticity associated with the upstream part of the starting jet is cancelled by the cross-flow boundary layer. Hairpin vortices are observed. At
$r<4$, the vorticity associated with the upstream part of the starting jet is cancelled by the cross-flow boundary layer. Hairpin vortices are observed. At  $r>4$, the starting jets penetrate through the boundary layer, and vortex rings are generated. They are asymmetric in shape as the windward vortex ring core is thinner due to the interaction with the cross-flow. As the limiting case of zero cross-flow (
$r>4$, the starting jets penetrate through the boundary layer, and vortex rings are generated. They are asymmetric in shape as the windward vortex ring core is thinner due to the interaction with the cross-flow. As the limiting case of zero cross-flow ( $r\rightarrow \infty$) is approached, the asymmetry decreases and the formation time corresponding to maximum vortex ring circulation converges to the characteristic value of
$r\rightarrow \infty$) is approached, the asymmetry decreases and the formation time corresponding to maximum vortex ring circulation converges to the characteristic value of  $t^*\approx 12$ recently determined for this type of non-parallel planar starting jets when emitted into quiescent surroundings (Steinfurth & Weiss, J. Fluid Mech., vol. 903, 2020, A16). The findings presented in the current article can promote the sophisticated selection of actuation parameters in active mixing and separation control.
$t^*\approx 12$ recently determined for this type of non-parallel planar starting jets when emitted into quiescent surroundings (Steinfurth & Weiss, J. Fluid Mech., vol. 903, 2020, A16). The findings presented in the current article can promote the sophisticated selection of actuation parameters in active mixing and separation control.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 15
- Cited by


