Article contents
Velocity-defect laws, log law and logarithmic friction law in the convective atmospheric boundary layer
Published online by Cambridge University Press: 26 November 2019
Abstract
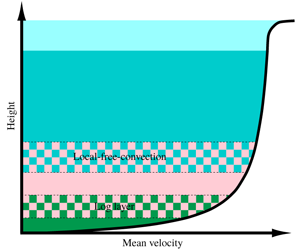
The mean velocity profile in the convective atmospheric boundary layer (CBL) is derived analytically. The shear-stress budget equations and the mean momentum equations are employed in the derivation. The multi-point Monin–Obukhov similarity (MMO) recently proposed and analytically derived by Tong & Nguyen (J. Atmos. Sci., vol. 72, 2015, pp. 4337–4348) and Tong & Ding (J. Fluid Mech., vol. 864, 2019, pp. 640–669) provides the scaling properties of the statistics in the shear-stress budget equations. Our previous and present studies have shown that the CBL is mathematically a singular perturbation problem. Therefore, we obtain the mean velocity profile using the method of matched asymptotic expansions. Three scaling layers are identified: the outer layer, which includes the mixed layer, the inner-outer layer and the inner-inner layer, which includes the roughness layer. There are two overlapping layers, the local-free-convection layer and the log layer, respectively. Two new velocity-defect laws are discovered: the mixed-layer velocity-defect law and the surface-layer velocity-defect law. The local-free-convection mean profile is obtained by asymptotically matching the expansions in the first two layers. The log law is obtained by matching the expansions in the last two layers. The von Kármán constant is obtained using velocity and length scales, and therefore has a physical interpretation. A new friction law, the convective logarithmic friction law, is obtained. The present work provides an analytical derivation of the mean velocity profile hypothesized in the Monin–Obukhov similarity theory, and is part of a comprehensive derivation of the MMO scaling from first principles.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 12
- Cited by


