Article contents
Very small insects use novel wing flapping and drag principle to generate the weight-supporting vertical force
Published online by Cambridge University Press: 19 September 2018
Abstract
The effect of air viscosity on the flow around an insect wing increases as insect size decreases. For the smallest insects (wing length 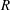 $R$ below 1 mm), the viscous effect is so large that lift-generation mechanisms used by their larger counterparts become ineffective. How the weight-supporting vertical force is generated is unknown. To elucidate the aerodynamic mechanisms responsible, we measure the wing kinematics of the tiny wasp Encarsia formosa (0.6 mm
$R$ below 1 mm), the viscous effect is so large that lift-generation mechanisms used by their larger counterparts become ineffective. How the weight-supporting vertical force is generated is unknown. To elucidate the aerodynamic mechanisms responsible, we measure the wing kinematics of the tiny wasp Encarsia formosa (0.6 mm 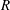 $R$) in hovering or very slow ascending flight and compute and analyse the aerodynamic forces. We find that the insects perform two unusual wing motions. One is ‘rowing’: the wings move fast downward and backward, like stroking oars. The other is the previously discovered Weis-Fogh ‘fling’. The rowing produces 70 % of the required vertical force and the Weis-Fogh ‘fling’ the other 30 %. The oaring wing mainly produces an approximately up-pointing drag, resulting in the vertical force. Because each oaring produces a starting flow, the drag is unsteady in nature and much greater than that in steady motion at the same velocities and angles of attack. Furthermore, our computation shows that if the tiny wasps employed the usual wing kinematics of the larger insects (flapping back and forth in a horizontal plane), the vertical force produced would be only
$R$) in hovering or very slow ascending flight and compute and analyse the aerodynamic forces. We find that the insects perform two unusual wing motions. One is ‘rowing’: the wings move fast downward and backward, like stroking oars. The other is the previously discovered Weis-Fogh ‘fling’. The rowing produces 70 % of the required vertical force and the Weis-Fogh ‘fling’ the other 30 %. The oaring wing mainly produces an approximately up-pointing drag, resulting in the vertical force. Because each oaring produces a starting flow, the drag is unsteady in nature and much greater than that in steady motion at the same velocities and angles of attack. Furthermore, our computation shows that if the tiny wasps employed the usual wing kinematics of the larger insects (flapping back and forth in a horizontal plane), the vertical force produced would be only 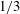 $1/3$ of that by the real wing kinematics; i.e. they must use the special wing movements to overcome the problem of large viscous effects encountered by the commonly used flapping kinematics. We have observed for the first time very small insects using drag to support their weight and we explain how a net vertical force is generated when the drag principle is applied.
$1/3$ of that by the real wing kinematics; i.e. they must use the special wing movements to overcome the problem of large viscous effects encountered by the commonly used flapping kinematics. We have observed for the first time very small insects using drag to support their weight and we explain how a net vertical force is generated when the drag principle is applied.
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
Cheng Supplementary Movie 1
Hover flight of EF1. The left, middle and right parts of the movie show the flight captured by the top-view camera and two side-view cameras, respectively. Playback speed is 15fps, approximately 0.15% of the actual speed of the movie.
- 80
- Cited by


