Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yang, Tao
Xia, Xi
and
Zhang, Peng
2019.
Vortex-dynamical interpretation of anti-phase and in-phase flickering of dual buoyant diffusion flames.
Physical Review Fluids,
Vol. 4,
Issue. 5,
Zhu, Xuren
Xia, Xi
and
Zhang, Peng
2020.
Stability of Buoyant Inverse Diffusion Methane Flames with Confinement Effects.
Combustion Science and Technology,
Vol. 192,
Issue. 9,
p.
1650.
Zhang, Xiaolei
Fang, Xu
Miao, Yanli
and
Hu, Longhua
2020.
Experimental study on pulsation frequency of free-, wall- and corner buoyant turbulent diffusion flames.
Fuel,
Vol. 276,
Issue. ,
p.
118022.
Kotov, M A
Lavrentyev, S Yu
Solovyov, N G
Shemyakin, A N
and
Yakimov, M Yu
2020.
Dynamics of laser plasma convective plume in high pressure xenon.
Journal of Physics: Conference Series,
Vol. 1675,
Issue. 1,
p.
012073.
Vadlamudi, Gautham
Thirumalaikumaran, S. K.
and
Basu, Saptarshi
2021.
Insights into the dynamics of wake flame in a freely falling droplet.
Physics of Fluids,
Vol. 33,
Issue. 12,
Wang, Guoqing
Liu, Xunchen
Xia, Xi
Wang, Shaojie
and
Qi, Fei
2021.
Dynamics of periodically-excited vortices in swirling flames.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 4,
p.
6183.
Pandey, Khushboo
Basu, Saptarshi
Krishan, Bal
and
V, Gautham
2021.
Dynamic self-tuning, flickering and shedding in buoyant droplet diffusion flames under acoustic excitation.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 2,
p.
3141.
Zhang, Haodong
Xia, Xi
and
Gao, Yi
2021.
Instability transition of a jet diffusion flame in quiescent environment.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 3,
p.
4971.
Mahesh Nayak, G.
Kolhe, Pankaj
and
Balusamy, Saravanan
2021.
Experimental study of buoyancy-induced instability in the DME and LPG jet diffusion flame.
Fuel,
Vol. 291,
Issue. ,
p.
120173.
Hosokawa, Yoshifumi
Nakashima, Erika
and
Ueno, Tomonaga
2021.
Image analysis of flame behavior for polyolefins and polystyrene in vertical flame test.
Journal of Applied Polymer Science,
Vol. 138,
Issue. 1,
Xia, Xi
Fu, Chen
Yang, Yifan
Yang, Xiaoyuan
Gao, Yi
and
Qi, Fei
2021.
Vortex formation and frequency tuning of periodically-excited jet diffusion flames.
Proceedings of the Combustion Institute,
Vol. 38,
Issue. 2,
p.
2067.
Thirumalaikumaran, S K
Vadlamudi, Gautham
and
Basu, Saptarshi
2022.
Insight into flickering/shedding in buoyant droplet-diffusion flame during interaction with vortex.
Combustion and Flame,
Vol. 240,
Issue. ,
p.
112002.
Kotov, Mikhail A
Lavrentyev, Sergey Yu
Shemyakin, Andrey N
Solovyov, Nikolay G
and
Yakimov, Mikhail Yu
2022.
Oscillations of convective flow around a continuous optical discharge in high-pressure xenon.
Plasma Sources Science and Technology,
Vol. 31,
Issue. 12,
p.
124002.
Nmira, Fatiha
and
Consalvi, Jean-Louis
2022.
Local contributions of resolved and subgrid turbulence-radiation interaction in LES/presumed FDF modelling of large-scale methanol pool fires.
International Journal of Heat and Mass Transfer,
Vol. 190,
Issue. ,
p.
122746.
Nayak, Guguloth Mahesh
Kolhe, Pankaj
and
Balusamy, Saravanan
2022.
Role of Buoyancy Induced Vortices in a Coupled-Mode of Oscillation in Laminar and Turbulent Jet Diffusion Flames.
Flow, Turbulence and Combustion,
Vol. 108,
Issue. 4,
p.
1069.
Zhang, Yajie
Yang, Yajing
Wei, Yanju
and
Liu, Shenghua
2022.
Vortex shedding controlled combustion of the wake flame of an n-heptane wetted porous sphere.
AIP Advances,
Vol. 12,
Issue. 10,
Zhao, Kun
Li, Situo
Lin, Ziming
Tang, Zhenhua
Qian, Jianan
Wang, Hua
Cui, Tong
and
Wang, Zhirong
2022.
Study on the global and spatial pulsation frequencies of rectangular syngas jet fire with different aspect ratios.
Fuel,
Vol. 330,
Issue. ,
p.
125558.
Lin, Kuo
Shen, Zhongjie
Liang, Qinfeng
Xu, Jianliang
and
Liu, Haifeng
2022.
The study of the effect of gas-phase fluctuation on slag flow and refractory brick corrosion in the slag tapping hole of an entrained-flow gasifier.
Chinese Journal of Chemical Engineering,
Vol. 47,
Issue. ,
p.
271.
Wang, Sirui
Zheng, Jianyi
Li, Lei
Yang, Zifeng
Xia, Xi
Fu, Chen
Gao, Yi
Liu, Xunchen
Han, Xiao
Zhang, Chi
and
Qi, Fei
2022.
Evolution characteristics of 3D vortex structures in stratified swirling flames studied by dual-plane stereoscopic PIV.
Combustion and Flame,
Vol. 237,
Issue. ,
p.
111874.
Araya, Yuki
Ito, Hiroaki
and
Kitahata, Hiroyuki
2022.
Bifurcation structure of the flame oscillation.
Physical Review E,
Vol. 105,
Issue. 4,
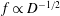 $f\propto D^{-1/2}$, where
$f\propto D^{-1/2}$, where 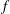 $f$ is the flickering frequency and
$f$ is the flickering frequency and 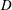 $D$ is the diameter of the fuel inlet. However, the connection between the toroidal vortex dynamics and the scaling has not been clearly understood. By incorporating the finding of Gharib et al. (J. Fluid Mech., vol. 360, 1998, pp. 121–140) that the detachment of a continuously growing vortex ring is inevitable and can be dictated by a universal constant that is essentially a non-dimensional circulation of the vortex, we theoretically established the connection between the periodicity of the toroidal vortices and the flickering of a buoyant diffusion flame with small Froude number. The scaling theory for flickering frequency was validated by the existing experimental data of pool flames and jet diffusion flames.
$D$ is the diameter of the fuel inlet. However, the connection between the toroidal vortex dynamics and the scaling has not been clearly understood. By incorporating the finding of Gharib et al. (J. Fluid Mech., vol. 360, 1998, pp. 121–140) that the detachment of a continuously growing vortex ring is inevitable and can be dictated by a universal constant that is essentially a non-dimensional circulation of the vortex, we theoretically established the connection between the periodicity of the toroidal vortices and the flickering of a buoyant diffusion flame with small Froude number. The scaling theory for flickering frequency was validated by the existing experimental data of pool flames and jet diffusion flames.

