Article contents
Vortex-induced vibration of a rotating sphere
Published online by Cambridge University Press: 20 December 2017
Abstract
Vortex-induced vibration (VIV) of a sphere represents one of the most generic fundamental fluid–structure interaction problems. Since vortex-induced vibration can lead to structural failure, numerous studies have focused on understanding the underlying principles of VIV and its suppression. This paper reports on an experimental investigation of the effect of imposed axial rotation on the dynamics of vortex-induced vibration of a sphere that is free to oscillate in the cross-flow direction, by employing simultaneous displacement and force measurements. The VIV response was investigated over a wide range of reduced velocities (i.e. velocity normalised by the natural frequency of the system): 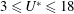 $3\leqslant U^{\ast }\leqslant 18$, corresponding to a Reynolds number range of
$3\leqslant U^{\ast }\leqslant 18$, corresponding to a Reynolds number range of 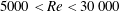 $5000<Re<30\,000$, while the rotation ratio, defined as the ratio between the sphere surface and inflow speeds,
$5000<Re<30\,000$, while the rotation ratio, defined as the ratio between the sphere surface and inflow speeds, 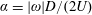 $\unicode[STIX]{x1D6FC}=|\unicode[STIX]{x1D714}|D/(2U)$, was varied in increments over the range of
$\unicode[STIX]{x1D6FC}=|\unicode[STIX]{x1D714}|D/(2U)$, was varied in increments over the range of  $0\leqslant \unicode[STIX]{x1D6FC}\leqslant 7.5$. It is found that the vibration amplitude exhibits a typical inverted bell-shaped variation with reduced velocity, similar to the classic VIV response for a non-rotating sphere but without the higher reduced velocity response tail. The vibration amplitude decreases monotonically and gradually as the imposed transverse rotation rate is increased up to
$0\leqslant \unicode[STIX]{x1D6FC}\leqslant 7.5$. It is found that the vibration amplitude exhibits a typical inverted bell-shaped variation with reduced velocity, similar to the classic VIV response for a non-rotating sphere but without the higher reduced velocity response tail. The vibration amplitude decreases monotonically and gradually as the imposed transverse rotation rate is increased up to 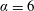 $\unicode[STIX]{x1D6FC}=6$, beyond which the body vibration is significantly reduced. The synchronisation regime, defined as the reduced velocity range where large vibrations close to the natural frequency are observed, also becomes narrower as
$\unicode[STIX]{x1D6FC}=6$, beyond which the body vibration is significantly reduced. The synchronisation regime, defined as the reduced velocity range where large vibrations close to the natural frequency are observed, also becomes narrower as  $\unicode[STIX]{x1D6FC}$ is increased, with the peak saturation amplitude observed at progressively lower reduced velocities. In addition, for small rotation rates, the peak amplitude decreases almost linearly with
$\unicode[STIX]{x1D6FC}$ is increased, with the peak saturation amplitude observed at progressively lower reduced velocities. In addition, for small rotation rates, the peak amplitude decreases almost linearly with  $\unicode[STIX]{x1D6FC}$. The imposed rotation not only reduces vibration amplitudes, but also makes the body vibrations less periodic. The frequency spectra revealed the occurrence of a broadband spectrum with an increase in the imposed rotation rate. Recurrence analysis of the structural vibration response demonstrated a transition from periodic to chaotic in a modified recurrence map complementing the appearance of broadband spectra at the onset of bifurcation. Despite considerable changes in flow structure, the vortex phase (
$\unicode[STIX]{x1D6FC}$. The imposed rotation not only reduces vibration amplitudes, but also makes the body vibrations less periodic. The frequency spectra revealed the occurrence of a broadband spectrum with an increase in the imposed rotation rate. Recurrence analysis of the structural vibration response demonstrated a transition from periodic to chaotic in a modified recurrence map complementing the appearance of broadband spectra at the onset of bifurcation. Despite considerable changes in flow structure, the vortex phase (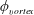 $\unicode[STIX]{x1D719}_{vortex}$), defined as the phase between the vortex force and the body displacement, follows the same pattern as for the non-rotating case, with the
$\unicode[STIX]{x1D719}_{vortex}$), defined as the phase between the vortex force and the body displacement, follows the same pattern as for the non-rotating case, with the  $\unicode[STIX]{x1D719}_{vortex}$ increasing gradually from low values in Mode I of the sphere vibration to almost
$\unicode[STIX]{x1D719}_{vortex}$ increasing gradually from low values in Mode I of the sphere vibration to almost 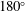 $180^{\circ }$ as the system undergoes a continuous transition to Mode II of the sphere vibration at higher reduced velocity. The total phase (
$180^{\circ }$ as the system undergoes a continuous transition to Mode II of the sphere vibration at higher reduced velocity. The total phase (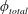 $\unicode[STIX]{x1D719}_{total}$), defined as the phase between the transverse lift force and the body displacement, only increases from low values after the peak amplitude response in Mode II has been reached. It reaches its maximum value (
$\unicode[STIX]{x1D719}_{total}$), defined as the phase between the transverse lift force and the body displacement, only increases from low values after the peak amplitude response in Mode II has been reached. It reaches its maximum value (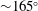 ${\sim}165^{\circ }$) close to the transition from the Mode II upper plateau to the lower plateau, reminiscent of the behaviour seen for the upper to lower branch transition for cylinder VIV. Hydrogen-bubble visualisations and particle image velocimetry (PIV) performed in the equatorial plane provided further insights into the flow dynamics near the sphere surface. The mean wake is found to be deflected towards the advancing side of the sphere, associated with an increase in the Magnus force. For higher rotation ratios, the near-wake rear recirculation zone is absent and the flow is highly vectored from the retreating side to the advancing side, giving rise to large-scale shedding. For a very high rotation ratio of
${\sim}165^{\circ }$) close to the transition from the Mode II upper plateau to the lower plateau, reminiscent of the behaviour seen for the upper to lower branch transition for cylinder VIV. Hydrogen-bubble visualisations and particle image velocimetry (PIV) performed in the equatorial plane provided further insights into the flow dynamics near the sphere surface. The mean wake is found to be deflected towards the advancing side of the sphere, associated with an increase in the Magnus force. For higher rotation ratios, the near-wake rear recirculation zone is absent and the flow is highly vectored from the retreating side to the advancing side, giving rise to large-scale shedding. For a very high rotation ratio of 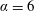 $\unicode[STIX]{x1D6FC}=6$, for which vibrations are found to be suppressed, a one-sided large-scale shedding pattern is observed, similar to the shear-layer instability one-sided shedding observed previously for a rigidly mounted rotating sphere.
$\unicode[STIX]{x1D6FC}=6$, for which vibrations are found to be suppressed, a one-sided large-scale shedding pattern is observed, similar to the shear-layer instability one-sided shedding observed previously for a rigidly mounted rotating sphere.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 50
- Cited by


