Article contents
Vortex-to-velocity reconstruction for wall-bounded turbulence via the field-based linear stochastic estimation
Published online by Cambridge University Press: 12 July 2021
Abstract
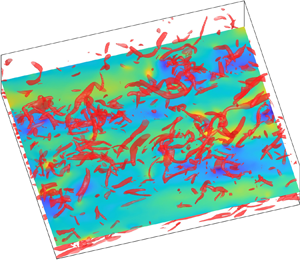
Representing complex flows by evolving vortex structures is an important principle in many investigations of wall-bounded turbulence. The practice of this principle benefits from the bi-directional transformation between the velocity field and the corresponding vortex field. While the velocity-to-vortex transformation could be implemented by various vortex identification criteria, few efforts have been devoted to the inverse process. This work develops a linear reconstruction method, which allows an effective reconstruction for the velocity field of wall turbulence based on a given vortex field. The vortex field is defined as a vector field by combining the swirl strength and the real eigenvector of the velocity gradient tensor. The reconstructed velocity fields are calculated by convolution operations on the vortex fields, with the kernel functions derived by the field-based linear stochastic estimation. The method can effectively recover the turbulent motions in a large scale range, showing clear advantages over the Biot–Savart formula in the near-wall region. The method is also employed to investigate the inducing effects of vortices at different heights. The wall-bounding effect on the induced motions is observed from the contribution spectra of vortices. The higher-order moments of the reconstructed streamwise velocity component present larger deviations from the original data, which is discussed and explained reasonably. At last, the vortex fields filtered by prescribed thresholds are employed to reconstruct the velocity fields. It is found that the strongest vortex components occupying 5 % of the total volume can reasonably recover the main flow features including both the near-wall streaks and the large-scale motions.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 8
- Cited by


