Article contents
Zonal flow in a resonant precessing cylinder
Published online by Cambridge University Press: 30 July 2021
Abstract
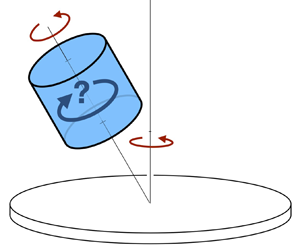
A cylinder undergoes precession when it rotates around its axis and this axis itself rotates around another axis. In a precessing cylinder full of fluid, a steady and axisymmetric component of the azimuthal flow is generally present. This component is called a zonal flow. Although zonal flows have been often observed in experiments and numerical simulations, their origin has eluded theoretical approaches so far. Here, we develop an asymptotic analysis to calculate the zonal flow forced in a resonant precessing cylinder, that is when the harmonic response is dominated by a single Kelvin mode. We find that the zonal flow originates from three different sources: (1) the nonlinear interaction of the inviscid Kelvin mode with its viscous correction; (2) the steady and axisymmetric response to the nonlinear interaction of the Kelvin mode with itself; and (3) the nonlinear interactions in the end boundary layers. In a precessing cylinder, two additional sources arise due to the equatorial Coriolis force and the forced shear flow; however, they cancel exactly. The study thus generalises to any Kelvin mode, forced by precession or any other mechanism. The present theoretical predictions of the zonal flow are confirmed by comparison with numerical simulations and experimental results. We also show numerically that the zonal flow is always retrograde in a resonant precessing cylinder ( $m=1$) or when it results from resonant Kelvin modes of azimuthal wavenumbers
$m=1$) or when it results from resonant Kelvin modes of azimuthal wavenumbers  $m=2$,
$m=2$,  $3$ and, presumably, higher.
$3$ and, presumably, higher.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 7
- Cited by


