Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T20:25:39.707Z Has data issue: false hasContentIssue false
  • English
  • Français

The acoustic impedance of a laminar viscous jet through a thin circular aperture

Published online by Cambridge University Press:  01 February 2019

David Fabre Open the ORCID record for David Fabre [Opens in a new window] ,
Raffaele Longobardi ,
Paul Bonnefis  and
Paolo Luchini Open the ORCID record for Paolo Luchini [Opens in a new window]
David Fabre*
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS, Allée Camille Soula, 31400 Toulouse, France
Raffaele Longobardi
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS, Allée Camille Soula, 31400 Toulouse, France DIIN (Dipartimento di Ingegneria Industriale), Universitá degli Studi di Salerno, Via Giovanni Paolo II, 84084 Fisciano (SA), Italy
Paul Bonnefis
Affiliation:
Institut de Mécanique des Fluides de Toulouse, IMFT, Université de Toulouse, CNRS, Allée Camille Soula, 31400 Toulouse, France
Paolo Luchini
Affiliation:
DIIN (Dipartimento di Ingegneria Industriale), Universitá degli Studi di Salerno, Via Giovanni Paolo II, 84084 Fisciano (SA), Italy
*
†Email address for correspondence: david.fabre@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The unsteady axisymmetric flow through a circular aperture in a thin plate subjected to harmonic forcing (for instance under the effect of an incident acoustic wave) is a classical problem first considered by Howe (Proc. R. Soc. Lond. A, vol. 366, 1979, pp. 205–223), using an inviscid model. The purpose of this work is to reconsider this problem through a numerical resolution of the incompressible linearized Navier–Stokes equations (LNSE) in the laminar regime, corresponding to 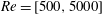$Re=[500,5000]$. We first compute a steady base flow which allows us to describe the vena contracta phenomenon in agreement with experiments. We then solve a linear problem allowing us to characterize both the spatial amplification of the perturbations and the impedance (or equivalently the Rayleigh conductivity), which is a key quantity to investigate the response of the jet to acoustic forcing. Since the linear perturbation is characterized by a strong spatial amplification, the numerical resolution requires the use of a complex mapping of the axial coordinate in order to enlarge the range of Reynolds number investigated. The results show that the impedances computed with 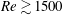$Re\gtrsim 1500$ collapse onto a single curve, indicating that a large Reynolds number asymptotic regime is effectively reached. However, expressing the results in terms of conductivity leads to substantial deviation with respect to Howe’s model. Finally, we investigate the case of finite-amplitude perturbations through direct numerical simulations (DNS). We show that the impedance predicted by the linear approach remains valid for amplitudes up to order 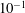$10^{-1}$, despite the fact that the spatial evolution of the perturbations in the jet is strongly nonlinear.

JFM classification

Acoustics: Hydrodynamic noise Wakes/Jets: Jets Acoustics: Jet noise
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 5 - 44
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abid, M., Brachet, M. & Huerre, P. 1993 Linear hydrodynamic instability of circular jets with thin shear layers. Eur. J. Mech. (B/Fluids) 12, 683.Google Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75 (5), 750.Google Scholar
Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14 (4), 529–551.Google Scholar
Bellucci, V., Flohr, P., Paschereit, C. O. & Magni, F. 2004 On the use of Helmholtz resonators for damping acoustic pulsations in industrial gas turbines. Trans ASME J. Engng Gas Turbines Power 126 (2), 271–275.Google Scholar
Bender, C. M. & Orszag, S. A. 2013 Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory. Springer Science & Business Media.Google Scholar
Boukir, K., Maday, Y., Métivet, B. & Razafindrakoto, E. 1997 A high-order characteristics/finite element method for the incompressible Navier–Stokes equations. Intl J. Numer. Meth. Fluids 25 (12), 1421–1454.Google Scholar
Charru, F. 2011 Hydrodynamic Instabilities, vol. 37. Cambridge University Press.Google Scholar
Colonius, T. 2004 Modeling artificial boundary conditions for compressible flow. Annu. Rev. Fluid Mech. 36, 315–345.Google Scholar
Crighton, D. G. 1985 The kutta condition in unsteady flow. Annu. Rev. Fluid Mech. 17 (1), 411–445.Google Scholar
Cummings, A. & Eversman, W. 1983 High amplitude acoustic transmission through duct terminations: theory. J. Sound Vib. 91 (4), 503–518.Google Scholar
Drazin, P. G. & Reid, W. H. 2004 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Eldredge, J. D., Bodony, D. J. & Shoeybi, M.2007 Numerical investigation of the acoustic behavior of a multi-perforated liner. In 13th AIAA/CEAS Aeroacoustics Conference (28th AIAA Aeroacoustics Conference). AIAA Paper 2007–3683.Google Scholar
Fabre, D., Bonnefis, P., Charru, F., Russo, S., Citro, V., Giannetti, F. & Luchini, P.2014 Application of global stability approaches to whistling jets and wind instruments. In International Symposium on Musical Acoustics (ISMA), Le Mans, France, July, pp. 7–12. Acoustical Society of America.Google Scholar
Fabre, D., Sabino, D. F., Citro, V., Bonnefis, P. & Giannetti, F. 2018 A practical review to linear and nonlinear approaches to flow instabilities. Appl. Mech. Rev. (in press).Google Scholar
Fabre, D., Sipp, D. & Jacquin, L. 2006 Kelvin waves and the singular modes of the Lamb–Oseen vortex. J. Fluid Mech. 551, 235–274.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.Google Scholar
Hecht, F. 2012 New development in freefem++. J. Numer. Math. 20 (3–4), 251–265.Google Scholar
Henrywood, R. H. & Agarwal, A. 2013 The aeroacoustics of a steam kettle. Phys. Fluids 25 (10), 107101.Google Scholar
Howe, M. S. 1979 On the theory of unsteady high Reynolds number flow through a circular aperture. Proc. R. Soc. Lond. A 366, 205–223.Google Scholar
Hughes, I. J. & Dowling, A. P. 1990 The absorption of sound by perforated linings. J. Fluid Mech. 218, 299–335.Google Scholar
Jeun, J., Nichols, J. W. & Jovanović, M. R. 2016 Input–output analysis of high-speed axisymmetric isothermal jet noise. Phys. Fluids 28 (4), 047101.Google Scholar
Jing, X. & Sun, X. 2000 Effect of plate thickness on impedance of perforated plates with bias flow. AIAA J. 38 (9), 1573–1578.Google Scholar
Jing, X. & Sun, X. 2002 Sound-excited flow and acoustic nonlinearity at an orifice. Phys. Fluids 14 (1), 268–276.Google Scholar
Kiya, M., Ido, Y. & Akiyama, H. 1996 Vortical structure in forced unsteady circular jet: simulation by 3D vortex method. In ESAIM: Proceedings, vol. 1, pp. 503–520. EDP Sciences.Google Scholar
Mann, A., Perot, F., Kim, M.-S. & Casalino, D. 2013 Characterization of acoustic liners absorption using a Lattice–Boltzmann method. In 19th AIAA/CEAS Aeroacoustics Conference, AIAA Paper 2013–2271.Google Scholar
Marquet, O., Sipp, D., Chomaz, J.-M. & Jacquin, L. 2008 Amplifier and resonator dynamics of a low-Reynolds-number recirculation bubble in a global framework. J. Fluid Mech. 605, 429–443.Google Scholar
Mendez, S. & Eldredge, J. D. 2009 Acoustic modeling of perforated plates with bias flow for large-eddy simulations. J. Comput. Phys. 228 (13), 4757–4772.10.1016/j.jcp.2009.03.026Google Scholar
Rayleigh, Lord 1945 The Theory of Sound. Dover.Google Scholar
Rupp, J., Carrotte, J. & Macquisten, M. 2012 The use of perforated damping liners in aero gas turbine combustion systems. Trans ASME J. Engng Gas Turbines Power 134 (7), 071502.Google Scholar
Sasaki, K., Piantanida, S., Cavalieri, A. V. G. & Jordan, P. 2017 Real-time modelling of wavepackets in turbulent jets. J. Fluid Mech. 821, 458–481.Google Scholar
Scarpato, A.2014 Linear and nonlinear analysis of the acoustic response of perforated plates traversed by a bias flow. PhD thesis, École Centrale Paris.Google Scholar
Scarpato, A., Ducruix, S. & Schuller, T.2011 A LES based sound absorption analysis of high-amplitude waves through an orifice with bias flow. In ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, pp. 613–622. American Society of Mechanical Engineers.Google Scholar
Scarpato, A., Tran, N., Ducruix, S. & Schuller, T. 2012 Modeling the damping properties of perforated screens traversed by a bias flow and backed by a cavity at low strouhal number. J. Sound Vib. 331 (2), 276–290.Google Scholar
Schmidt, O. T., Towne, A., Colonius, T., Cavalieri, A. V. G., Jordan, P. & Brès, G. A. 2017 Wavepackets and trapped acoustic modes in a turbulent jet: coherent structure eduction and global stability. J. Fluid Mech. 825, 1153–1181.Google Scholar
Schmidt, O. T., Towne, A., Rigas, G., Colonius, T. & Brès, G. A. 2018 Spectral analysis of jet turbulence. J. Fluid Mech. 855, 953–982.Google Scholar
Semeraro, O., Lesshafft, L., Jaunet, V. & Jordan, P. 2016 Modeling of coherent structures in a turbulent jet as global linear instability wavepackets: theory and experiment. Intl J. Heat Fluid Flow 62, 24–32.Google Scholar
Shaabani-Ardali, L., Sipp, D. & Lesshafft, L. 2017 Time-delayed feedback technique for suppressing instabilities in time-periodic flow. Phys. Rev. Fluids 2 (11), 113904.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.10.1017/S0022112007008907Google Scholar
Smith, D. & Walker, W. J. 1923 Orifice flow. Proc. Inst. Mech. Engrs 104 (1), 23–36.Google Scholar
Su, J., Rupp, J., Garmory, A. & Carrotte, J. F. 2015 Measurements and computational fluid dynamics predictions of the acoustic impedance of orifices. J. Sound Vib. 352, 174–191.Google Scholar
Tam, C. K. W., Ju, H., Jones, M. G., Watson, W. R. & Parrott, T. L. 2005 A computational and experimental study of slit resonators. J. Sound Vib. 284 (3–5), 947–984.Google Scholar
Tam, W., Christopher, K. & Kurbatskii, K. A. 2000 Microfluid dynamics and acoustics of resonant liners. AIAA J. 38 (8), 1331–1339.Google Scholar
Yang, D. & Morgans, A. S. 2016 A semi-analytical model for the acoustic impedance of finite length circular holes with mean flow. J. Sound Vib. 384, 294–311.Google Scholar
Yang, D. & Morgans, A. S. 2017 The acoustics of short circular holes opening to confined and unconfined spaces. J. Sound Vib. 393, 41–61.Google Scholar
Zhang, Q. & Bodony, D. J. 2016 Numerical investigation of a honeycomb liner grazed by laminar and turbulent boundary layers. J. Fluid Mech. 792, 936–980.Google Scholar