Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T23:03:47.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Acoustic streaming and the induced forces between two spheres

Published online by Cambridge University Press:  25 November 2016

D. Fabre ,
J. Jalal ,
J. S. Leontini  and
R. Manasseh
D. Fabre*
Affiliation:
Université de Toulouse, INPT, UPS, IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France
J. Jalal
Affiliation:
Faculty of Science, Engineering and Technology, Swinburne University of Technology, Hawthorn, Victoria 3122, Australia
J. S. Leontini
Affiliation:
Faculty of Science, Engineering and Technology, Swinburne University of Technology, Hawthorn, Victoria 3122, Australia
R. Manasseh
Affiliation:
Faculty of Science, Engineering and Technology, Swinburne University of Technology, Hawthorn, Victoria 3122, Australia
*
†Email address for correspondence: david.fabre@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The ability of acoustic microstreaming to cause a pair of particles to attract or repel is investigated. Expanding the flow around two spheres in terms of a small-amplitude parameter measuring the amplitude of the forcing, the leading order is an oscillating flow field with zero mean representing the effect of the applied acoustic field, while the second-order correction contains a steady streaming component. A modal decomposition in the azimuthal direction reduces the problem to a few linear problems in a two-dimensional domain corresponding to the meridional (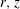$r,z$) plane. The analysis computes both the intricate flow fields and the mean forces felt by both spheres. If the spheres are aligned obliquely with respect to the oscillating flow, they experience a lateral force which realigns them into a transverse configuration. In this transverse configuration, they experience an axial force which can be either attractive or repulsive. At high frequencies the force is always attractive. At low frequencies, it is repulsive. At intermediate frequencies, the force is attractive at large distances and repulsive at small distances, leading to the existence of a stable equilibrium configuration.

JFM classification

Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Micro-/Nano-fluid dynamics: Microfluidics Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 810 , 10 January 2017 , pp. 378 - 391
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Doinikov, A. A. & Bouakaz, A. 2010 Acoustic microstreaming around a gas bubble. J. Acoust. Soc. Am. 127 (2), 703–709.CrossRefGoogle ScholarPubMed
Gormley, G. & Wu, J. R. 1998 Observation of acoustic streaming near Albunex (R) spheres. J. Acoust. Soc. Am. 104, 3115–3118.Google Scholar
Klotsa, D., Swift, M. R., Bowley, R. M. & King, P. J. 2007 Interaction of spheres in oscillatory fluid flows. Phys. Rev. E 76, 056314.CrossRefGoogle ScholarPubMed
Kolb, J. & Nyborg, W. L. 1956 Small-scale acoustic streaming in liquids. J. Acoust. Soc. Am. 28, 1237.CrossRefGoogle Scholar
Lane, C. A. 1955 Acooustical streaming in the vicinity of a sphere. J. Acoust. Soc. Am. 27 (6), 1082–1086.Google Scholar
Leong, T., Collis, J., Manasseh, R., Ooi, A., Novell, A., Bouakaz, A., Ashokkumar, M. & Kentish, S. 2011 The role of surfactant head group, chain length and cavitation microstreaming on the growth of bubbles by rectified diffusion. J. Phys. Chem. 115 (49), 24310–24316.Google Scholar
Leong, T., Johansson, L., Juliano, P., McArthur, S. & Manasseh, R. 2013 Ultrasonic separation of particulate fluids in small and large scale systems: a review. Ind. Engng Chem. Res. 52 (47), 16555–16576.Google Scholar
Manasseh, R. 2015 Fundamental aspects of acoustic bubbles, acoustic streaming, and cavitation microstreaming. In Handbook of Ultrasonics and Sonochemistry (ed. Yasui, K. & Ashokkumar, M.), chap. 1, pp. 1–37. Springer.Google Scholar
Rayleigh, Lord 1884 On the circulation of air observed in Kundt’s tubes, and on some allied acoustical problems. Phil. Trans. R. Soc. Lond. 175, 1–21.Google Scholar
Riley, N. 1966 On a sphere oscillating in a viscous fluid. Q. J. Mech. Appl. Maths 19 (4), 461–472.Google Scholar
Riley, N. 2001 Steady streaming. Annu. Rev. Fluid Mech. 33, 43–65.Google Scholar
Stokes, G. G. 1851 On the Effect of the Internal Friction of Fluids on the Motion of Pendulums, vol. 9. Pitt Press.Google Scholar
Tho, P., Manasseh, R. & Ooi, A. 2007 Cavitation microstreaming in single and multiple bubble systems. J. Fluid Mech. 576, 191–233.Google Scholar
Wang, C. & Chen, J. 2013 Cavitation microstreaming generated by a bubble pair in an ultrasound field. J. Acoust. Soc. Am. 134 (2), 1675–1682.Google Scholar
Wu, J. R. & Du, G. H. 1997 Streaming generated by a bubble in an ultrasound field. J. Acoust. Soc. Am. 101 (4), 1899–1907.Google Scholar