1. Introduction
When a fluid system is exposed to a periodic stimulation, the fluid's reaction is not solely periodic. Instead, it is marked by a blend of periodic fluid motion and a steady Stokes drift component. In the context of acoustically actuated fluid systems, the periodic component corresponds to an acoustic wave, while the steady component is commonly known as acoustic streaming. Theoretical analyses of acoustic streaming have a long and rich history, dating back to the pioneering work of Rayleigh (Reference Rayleigh1884). One of the primary challenges concerning acoustic streaming stems from the large disparity between the length and time scales of the periodic and mean flow; this makes a direct solution of the Navier–Stokes equations computationally intractable unless weakening assumptions are employed to avoid contributions from interfaces and boundary layer flows. To tackle this, Rayleigh (Reference Rayleigh1884) proposed a Mach number-based expansion approach to segregate the total fluid response into different components, with zeroth-order components denoting the flow in absence of acoustic actuation, first-order components denoting periodic flow and the second-order components denoting the time-averaged steady flow. This approach results in a computationally tractable, one-way coupled system of equations that continues to form the bedrock of most acoustic streaming investigations (Vanneste & Bühler Reference Vanneste and Bühler2011; Chini, Malecha & Dreeben Reference Chini, Malecha and Dreeben2014; Nama, Huang & Costanzo Reference Nama, Huang and Costanzo2017). However, as pointed in several reports (Rudenko & Soluyan Reference Rudenko and Soluyan1971; Zarembo Reference Zarembo1971; Lighthill Reference Lighthill1978), this approach is applicable only to slow acoustic streaming, where the mean flow velocity is small in comparison with the periodic flow (or acoustic wave) velocity and the steady drift flow (or streaming) driven fluid momentum does not significantly impact the acoustic wave.
Recent acoustofluidic systems that employ acoustic waves with high frequencies and high powers have revealed the existence of mean flows with velocities that are of similar magnitude to the periodic flows (Kamakura et al. Reference Kamakura, Sudo, Matsuda and Kumamoto1996; Dentry, Yeo & Friend Reference Dentry, Yeo and Friend2014). These observations necessitate the development of a theory that can account for the generation of acoustic streaming at finite Reynolds number due to convective effects in an acoustic wave, while the wave is simultaneously impacted by the streaming. Dubrovski, Friend & Manor (Reference Dubrovski, Friend and Manor2023) address this issue by developing a novel theoretical framework to study acoustic streaming at arbitrary Reynolds number, and performing a scaling analysis to provide crucial insights into this class of acoustic streaming.
2. Overview
The article by Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) systematically extends the ideas of Zarembo (Reference Zarembo1971) to obtain the governing equations for the periodic and steady flow components. To this end, they employ three postulates: (i) all flow field variables are considered to be the sum of steady and transient components, (ii) the transient components are taken to be periodic in time and (iii) the Mach number is assumed to be small such that the periodic density component is assumed to be small relative to the steady density component. Crucially, they do not require the periodic velocity to be smaller than the steady velocity – a critical feature of the classical slow-streaming theories. Instead, the periodic velocity, 
$\boldsymbol {u}_p$, and the steady velocity, $\boldsymbol {u}_s$, are taken to be of similar magnitude, i.e. ${O}(\boldsymbol {u}_p)\approx {O}(\boldsymbol {u}_s)$.
The equations for the conservation of mass and momentum are time averaged to obtain equations for the steady flow component with arbitrary hydrodynamic Reynolds number. Correspondingly, the nonlinear periodic flow equations are obtained by subtracting the time-averaged equations from the full conservation equations. It is important to note that, since the periodic and steady velocities are taken to be of similar magnitude, the periodic flow equations include steady convective contributions to the periodic flow. This results in a two-way coupled system of equations where momentum flows in both directions between the periodic and steady flow components, in contrast to the slow-streaming equations where the momentum flows from the periodic flow component to the steady component but not vice versa. A scaling analysis of these governing equations shows that a distance of approximately ${St}\,\kappa ^{-1}$ from the acoustic source is required for significant cumulative distortion of the periodic flow due to convective effects, where ${St}=\omega /(U \kappa )$ is the Strouhal number with $\kappa$, $\omega$ and $U$ being the wavenumber, angular frequency and characteristic velocity of the periodic flow, respectively.
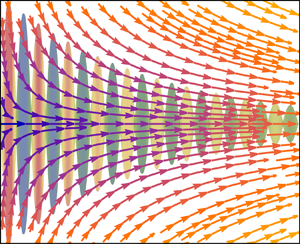
To highlight the insights from the scaling analysis and demonstrate specific features of fast streaming in comparison with slow streaming, Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) consider a case study along the lines of Rudenko & Soluyan (Reference Rudenko and Soluyan1971). Specifically, they consider a two-dimensional flow generated in a liquid between a thickness mode vibrator and a solid obstacle of similar acoustic impedance (see figure 1). The system is considered to be symmetric with the line of symmetry passing through the middle of the acoustic vibrator ($x$ axis in figure 1). Further, the system is open along the $y$ direction such that the acoustic wave vanishes as the magnitude of $y$ coordinate reaches infinity. This configuration allows for the study of acoustic streaming along the line of symmetry by simplifying the lateral contributions: the periodic flow is taken to be quasi-planar near the axis of symmetry, and the leading-order flow perpendicular to the axis of symmetry is considered to be quadratic.
Figure 1. Schematic of the model system which is symmetric about the $x$ axis, where acoustic waves are generated by an acoustic horn at $x = 0$, produce acoustic streaming as they attenuate and absorb in a solid obstacle – an acoustic absorber – at $x = l$. Adapted from Dubrovski et al. (Reference Dubrovski, Friend and Manor2023).
For asymptotically large hydrodynamic Reynolds number, $\textit {Re}=\rho _s U/(\mu \kappa )$ with $\rho _s$ and $\mu$ being the steady density component and shear viscosity of the liquid, the convection of momentum governs the streaming flow away from the interfaces. In this scenario, the case study reveals that the steady flow reaches a velocity magnitude comparable to the periodic flow at a distance equal to the inverse of the periodic flow attenuation length from the acoustic source. A numerical analysis for the case with small to moderate Reynolds number ($\textit {Re}\leqslant 1$) reveals that the asymptotic approach for small $\textit {Re}$ models both the periodic wave and flow sufficiently well for $\textit {Re}\leqslant 1$. In this regime, the acoustic wave dominates the total flow, irrespective of the distance from the acoustic source. The situation is different for $\textit {Re}\gg 1$, where the flow is dominated by the acoustic wave only in the proximity of the acoustic source. In this regime, once the acoustic wave is largely attenuated at sufficiently far distances from the acoustic source, the flow field is governed completely by the steady flow.
The key take-away messages for the readers can be summarized as follows: the theoretical framework by Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) allows the consideration of the fast-streaming regime, where the streaming flow generated by an acoustic wave can alter the wave itself. Close to the acoustic source, the steady flow velocity is small compared with the periodic flow velocity for all values of $\textit {Re}$ and the system can be viewed as a one-way coupled system with momentum flowing from the periodic flow component to the steady flow component. At larger distances from the acoustic source, the behaviour depends on the magnitude of $\textit {Re}$. Here, for small $\textit {Re}$, the flow is still dominated by the periodic flow component. In contrast, for large $\textit {Re}$ and at sufficiently large distances from the acoustic source, the system becomes a two-way coupled system where both the periodic flow and the streaming alter each other. Perhaps, the most important contribution of this study lies in the proposed theoretical foundation that expounds the conceptual ideas put forward by Zarembo (Reference Zarembo1971) to systematically derive a set of governing equations for the fast streaming regime.
3. Outlook and future directions
The study by Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) tackles a long-standing issue in the field of acoustic streaming concerning the inadequacy of the current streaming theories for describing the fast-streaming regime where the streaming flow significantly impacts the acoustic wave that gives rise to it. The proposed approach provides the foundational framework to handle the fast-streaming regime, and will undoubtedly spur new computational investigations into the contributions of the steady flow to the periodic flow in cases of drift of mass near a surface in contact with standing/travelling waves. Given the numerical challenges associated with the two-way coupled nature of the governing equations for the periodic and steady flow, it will also be interesting to see if numerical solutions can be attempted for non-axisymmetric cases or two-dimensional closed channels where the flow might be generated due to changes in sound wave intensity in different directions. Lastly, the fundamental approach presented in this work will benefit other disciplines that are characterized by coupled phenomena at multiple scales, including biological growth and remodelling (Latorre & Humphrey Reference Latorre and Humphrey2018; Gharahi et al. Reference Gharahi, Filonova, Mullagura, Nama, Baek and Figueroa2023), structural mechanics (Aubry & Puel Reference Aubry and Puel2010) and reactive transport (Molins & Knabner Reference Molins and Knabner2019).
$x$ axis, where acoustic waves are generated by an acoustic horn at 
$x = 0$, produce acoustic streaming as they attenuate and absorb in a solid obstacle – an acoustic absorber – at 
$x = l$. Adapted from Dubrovski et al. (2023).
You have
Access
1. Introduction
When a fluid system is exposed to a periodic stimulation, the fluid's reaction is not solely periodic. Instead, it is marked by a blend of periodic fluid motion and a steady Stokes drift component. In the context of acoustically actuated fluid systems, the periodic component corresponds to an acoustic wave, while the steady component is commonly known as acoustic streaming. Theoretical analyses of acoustic streaming have a long and rich history, dating back to the pioneering work of Rayleigh (Reference Rayleigh1884). One of the primary challenges concerning acoustic streaming stems from the large disparity between the length and time scales of the periodic and mean flow; this makes a direct solution of the Navier–Stokes equations computationally intractable unless weakening assumptions are employed to avoid contributions from interfaces and boundary layer flows. To tackle this, Rayleigh (Reference Rayleigh1884) proposed a Mach number-based expansion approach to segregate the total fluid response into different components, with zeroth-order components denoting the flow in absence of acoustic actuation, first-order components denoting periodic flow and the second-order components denoting the time-averaged steady flow. This approach results in a computationally tractable, one-way coupled system of equations that continues to form the bedrock of most acoustic streaming investigations (Vanneste & Bühler Reference Vanneste and Bühler2011; Chini, Malecha & Dreeben Reference Chini, Malecha and Dreeben2014; Nama, Huang & Costanzo Reference Nama, Huang and Costanzo2017). However, as pointed in several reports (Rudenko & Soluyan Reference Rudenko and Soluyan1971; Zarembo Reference Zarembo1971; Lighthill Reference Lighthill1978), this approach is applicable only to slow acoustic streaming, where the mean flow velocity is small in comparison with the periodic flow (or acoustic wave) velocity and the steady drift flow (or streaming) driven fluid momentum does not significantly impact the acoustic wave.
Recent acoustofluidic systems that employ acoustic waves with high frequencies and high powers have revealed the existence of mean flows with velocities that are of similar magnitude to the periodic flows (Kamakura et al. Reference Kamakura, Sudo, Matsuda and Kumamoto1996; Dentry, Yeo & Friend Reference Dentry, Yeo and Friend2014). These observations necessitate the development of a theory that can account for the generation of acoustic streaming at finite Reynolds number due to convective effects in an acoustic wave, while the wave is simultaneously impacted by the streaming. Dubrovski, Friend & Manor (Reference Dubrovski, Friend and Manor2023) address this issue by developing a novel theoretical framework to study acoustic streaming at arbitrary Reynolds number, and performing a scaling analysis to provide crucial insights into this class of acoustic streaming.
2. Overview
The article by Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) systematically extends the ideas of Zarembo (Reference Zarembo1971) to obtain the governing equations for the periodic and steady flow components. To this end, they employ three postulates: (i) all flow field variables are considered to be the sum of steady and transient components, (ii) the transient components are taken to be periodic in time and (iii) the Mach number is assumed to be small such that the periodic density component is assumed to be small relative to the steady density component. Crucially, they do not require the periodic velocity to be smaller than the steady velocity – a critical feature of the classical slow-streaming theories. Instead, the periodic velocity,
$\boldsymbol {u}_p$, and the steady velocity, 
$\boldsymbol {u}_s$, are taken to be of similar magnitude, i.e. 
${O}(\boldsymbol {u}_p)\approx {O}(\boldsymbol {u}_s)$.
The equations for the conservation of mass and momentum are time averaged to obtain equations for the steady flow component with arbitrary hydrodynamic Reynolds number. Correspondingly, the nonlinear periodic flow equations are obtained by subtracting the time-averaged equations from the full conservation equations. It is important to note that, since the periodic and steady velocities are taken to be of similar magnitude, the periodic flow equations include steady convective contributions to the periodic flow. This results in a two-way coupled system of equations where momentum flows in both directions between the periodic and steady flow components, in contrast to the slow-streaming equations where the momentum flows from the periodic flow component to the steady component but not vice versa. A scaling analysis of these governing equations shows that a distance of approximately
${St}\,\kappa ^{-1}$ from the acoustic source is required for significant cumulative distortion of the periodic flow due to convective effects, where 
${St}=\omega /(U \kappa )$ is the Strouhal number with 
$\kappa$, 
$\omega$ and 
$U$ being the wavenumber, angular frequency and characteristic velocity of the periodic flow, respectively.
To highlight the insights from the scaling analysis and demonstrate specific features of fast streaming in comparison with slow streaming, Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) consider a case study along the lines of Rudenko & Soluyan (Reference Rudenko and Soluyan1971). Specifically, they consider a two-dimensional flow generated in a liquid between a thickness mode vibrator and a solid obstacle of similar acoustic impedance (see figure 1). The system is considered to be symmetric with the line of symmetry passing through the middle of the acoustic vibrator (
$x$ axis in figure 1). Further, the system is open along the 
$y$ direction such that the acoustic wave vanishes as the magnitude of 
$y$ coordinate reaches infinity. This configuration allows for the study of acoustic streaming along the line of symmetry by simplifying the lateral contributions: the periodic flow is taken to be quasi-planar near the axis of symmetry, and the leading-order flow perpendicular to the axis of symmetry is considered to be quadratic.
Figure 1. Schematic of the model system which is symmetric about the
$x$ axis, where acoustic waves are generated by an acoustic horn at 
$x = 0$, produce acoustic streaming as they attenuate and absorb in a solid obstacle – an acoustic absorber – at 
$x = l$. Adapted from Dubrovski et al. (Reference Dubrovski, Friend and Manor2023).
For asymptotically large hydrodynamic Reynolds number,
$\textit {Re}=\rho _s U/(\mu \kappa )$ with 
$\rho _s$ and 
$\mu$ being the steady density component and shear viscosity of the liquid, the convection of momentum governs the streaming flow away from the interfaces. In this scenario, the case study reveals that the steady flow reaches a velocity magnitude comparable to the periodic flow at a distance equal to the inverse of the periodic flow attenuation length from the acoustic source. A numerical analysis for the case with small to moderate Reynolds number (
$\textit {Re}\leqslant 1$) reveals that the asymptotic approach for small 
$\textit {Re}$ models both the periodic wave and flow sufficiently well for 
$\textit {Re}\leqslant 1$. In this regime, the acoustic wave dominates the total flow, irrespective of the distance from the acoustic source. The situation is different for 
$\textit {Re}\gg 1$, where the flow is dominated by the acoustic wave only in the proximity of the acoustic source. In this regime, once the acoustic wave is largely attenuated at sufficiently far distances from the acoustic source, the flow field is governed completely by the steady flow.
The key take-away messages for the readers can be summarized as follows: the theoretical framework by Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) allows the consideration of the fast-streaming regime, where the streaming flow generated by an acoustic wave can alter the wave itself. Close to the acoustic source, the steady flow velocity is small compared with the periodic flow velocity for all values of
$\textit {Re}$ and the system can be viewed as a one-way coupled system with momentum flowing from the periodic flow component to the steady flow component. At larger distances from the acoustic source, the behaviour depends on the magnitude of 
$\textit {Re}$. Here, for small 
$\textit {Re}$, the flow is still dominated by the periodic flow component. In contrast, for large 
$\textit {Re}$ and at sufficiently large distances from the acoustic source, the system becomes a two-way coupled system where both the periodic flow and the streaming alter each other. Perhaps, the most important contribution of this study lies in the proposed theoretical foundation that expounds the conceptual ideas put forward by Zarembo (Reference Zarembo1971) to systematically derive a set of governing equations for the fast streaming regime.
3. Outlook and future directions
The study by Dubrovski et al. (Reference Dubrovski, Friend and Manor2023) tackles a long-standing issue in the field of acoustic streaming concerning the inadequacy of the current streaming theories for describing the fast-streaming regime where the streaming flow significantly impacts the acoustic wave that gives rise to it. The proposed approach provides the foundational framework to handle the fast-streaming regime, and will undoubtedly spur new computational investigations into the contributions of the steady flow to the periodic flow in cases of drift of mass near a surface in contact with standing/travelling waves. Given the numerical challenges associated with the two-way coupled nature of the governing equations for the periodic and steady flow, it will also be interesting to see if numerical solutions can be attempted for non-axisymmetric cases or two-dimensional closed channels where the flow might be generated due to changes in sound wave intensity in different directions. Lastly, the fundamental approach presented in this work will benefit other disciplines that are characterized by coupled phenomena at multiple scales, including biological growth and remodelling (Latorre & Humphrey Reference Latorre and Humphrey2018; Gharahi et al. Reference Gharahi, Filonova, Mullagura, Nama, Baek and Figueroa2023), structural mechanics (Aubry & Puel Reference Aubry and Puel2010) and reactive transport (Molins & Knabner Reference Molins and Knabner2019).
Declaration of interest
The author reports no conflict of interest.