Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-30T21:49:50.894Z Has data issue: false hasContentIssue false
  • English
  • Français

Active attenuation of a trailing vortex inspired by a parabolized stability analysis

Published online by Cambridge University Press:  19 September 2018

Adam M. Edstrand Open the ORCID record for Adam M. Edstrand [Opens in a new window] ,
Yiyang Sun Open the ORCID record for Yiyang Sun [Opens in a new window] ,
Peter J. Schmid Open the ORCID record for Peter J. Schmid [Opens in a new window] ,
Kunihiko Taira Open the ORCID record for Kunihiko Taira [Opens in a new window]  and
Louis N. Cattafesta III Open the ORCID record for Louis N. Cattafesta III [Opens in a new window]
Adam M. Edstrand
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, Florida State University, Tallahassee, FL 32310, USA
Yiyang Sun
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, Florida State University, Tallahassee, FL 32310, USA
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
Kunihiko Taira
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, Florida State University, Tallahassee, FL 32310, USA
Louis N. Cattafesta III*
Affiliation:
Department of Mechanical Engineering, Florida Center for Advanced Aero-Propulsion, Florida State University, Tallahassee, FL 32310, USA
*
†Email address for correspondence: lcattafesta@fsu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

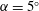Designing effective control for complex three-dimensional flow fields proves to be non-trivial. Often, intuitive control strategies lead to suboptimal control. To navigate the control space, we use a linear parabolized stability analysis to guide the design of a control scheme for a trailing vortex flow field aft of a NACA0012 half-wing at an angle of attack $\unicode[STIX]{x1D6FC}=5^{\circ }$ and a chord-based Reynolds number 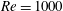$Re=1000$. The stability results show that the unstable mode with the smallest growth rate (fifth wake mode) provides a pathway to excite a vortex instability, whereas the principal unstable mode does not. Inspired by this finding, we perform direct numerical simulations that excite each mode with body forces matching the shape function from the stability analysis. Relative to the uncontrolled case, the controlled flows show increased attenuation of circulation and peak streamwise vorticity, with the fifth-mode-based control set-up outperforming the principal-mode-based set-up. From these results, we conclude that a rudimentary linear stability analysis can provide key insights into the underlying physics and help engineers design effective physics-based flow control strategies.

JFM classification

Flow Control: Flow Control Flow Control: Instability control Vortex Flows: Vortex instability
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , R2
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.Google Scholar
Crouch, J. 2005 Airplane trailing vortices and their control. C. R. Phys. 6 (4–5), 487–499.Google Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wing-tip vortex. J. Fluid Mech. 312, 67–106.Google Scholar
Edstrand, A. & Cattafesta, L. N. 2015 Topology of a trailing vortex flow field with steady circulation control blowing. In 53rd AIAA Aerospace Sciences Meeting, AIAA-2015-1706. American Institute of Aeronautics and Astronautics.Google Scholar
Edstrand, A. M., Davis, T. B., Schmid, P. J., Taira, K. & Cattafesta, L. N. 2016 On the mechanism of trailing vortex wandering. J. Fluid Mech. 801, R1–11.Google Scholar
Edstrand, A. M., Schmid, P. J., Taira, K. & Cattafesta, L. N. 2018 A parallel stability analysis of a trailing vortex wake. J. Fluid Mech. 837, 858–895.Google Scholar
Ham, F. & Iaccarino, G. 2004 Energy Conservation in Collocated Discretization Schemes on Unstructured Meshes, pp. 3–14. Annual Research Brief, Center for Turbulence Research, Stanford University.Google Scholar
Ham, F., Mattsson, K. & Iaccarino, G. 2006 Accurate and Stable Finite Volume Operators for Unstructured Flow Solvers, pp. 243–261. Annual Research Brief, Center for Turbulence Research, Stanford University.Google Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29, 245–283.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proc. of the Summer Program, pp. 193–208. Center of Turbulence Research.Google Scholar
Jacquin, L., Fabre, D., Geffroy, P. & Coustols, E. 2001 The properties of a transport aircraft wake in the extended near field: an experimental study. In 39th AIAA Aerospace Sciences Meeting, AIAA-2001-1038. American Institute of Aeronautics and Astronautics.Google Scholar
Khorrami, M. R. 1991 On the viscous modes of instability of a trailing line vortex. J. Fluid Mech. 225, 197–212.Google Scholar
Kim, J. & Bewley, T. R. 2007 A linear systems approach to flow control. Annu. Rev. Fluid Mech. 39 (1), 383–417.Google Scholar
Margaris, P. & Gursul, I. 2006 Wing tip vortex control using synthetic jets. Aeronaut. J. 110 (1112), 673–681.Google Scholar
Margaris, P. & Gursul, I. 2010 Vortex topology of wing tip blowing. Aerosp. Sci. Technol. 14, 143–160.Google Scholar
Matalanis, C. G. & Eaton, J. K. 2007 Wake vortex alleviation using rapidly actuated segmented Gurney flaps. AIAA J. 45 (8), 1874–1884.Google Scholar
Mayer, E. & Powell, K. 1992 Viscous and inviscid instabilities of a trailing vortex. J. Fluid Mech. 245, 91–114.Google Scholar
Paredes, P., Theofilis, V., Rodríguez, D. & Tendero, J. 2011 The PSE-3D instability analysis methodology for flows depending strongly on two and weakly on the third spatial dimension. In 6th AIAA Theoretical Fluid Mechanics Conference, AIAA-2011-3752. American Institute of Aeronautics and Astronautics.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656 (10), 5–28.Google Scholar
Spalart, P. R. 1998 Airplane trailing vortices. Annu. Rev. Fluid Mech. 30 (1), 107–138.Google Scholar
Streett, C. L., Lockard, D. P., Singer, B. A., Khorrami, M. R. & Choudhari, M. M. 2003 In search of the physics: the interplay of experiment and computation in airframe noise research: flap-edge noise. In 41st Aerospace Sciences Meeting and Exhibit, AIAA-2003-0979. American Institute of Aeronautics and Astronautics.Google Scholar
Taira, K. & Colonius, T. 2009 Effect of tip vortices and low-Reynolds-number poststall flow control. AIAA J. 47 (3), 749–756.Google Scholar