Article contents
Aerodynamics of planar counterflowing jets
Published online by Cambridge University Press: 16 May 2017
Abstract
The planar laminar flow resulting from the impingement of two gaseous jets of different density issuing into an open space from aligned steadily fed slot nozzles of semi-width 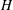 $H$ separated by a distance
$H$ separated by a distance 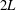 $2L$ is investigated by numerical and analytical methods. Specific consideration is given to the high Reynolds and low Mach number conditions typically present in counterflow-flame experiments, for which the flow is nearly inviscid and incompressible. It is shown that introduction of a density-weighted vorticity–streamfunction formulation effectively reduces the problem to one involving two jets of equal density, thereby removing the vortex-sheet character of the interface separating the two jet streams. Besides the geometric parameter
$2L$ is investigated by numerical and analytical methods. Specific consideration is given to the high Reynolds and low Mach number conditions typically present in counterflow-flame experiments, for which the flow is nearly inviscid and incompressible. It is shown that introduction of a density-weighted vorticity–streamfunction formulation effectively reduces the problem to one involving two jets of equal density, thereby removing the vortex-sheet character of the interface separating the two jet streams. Besides the geometric parameter 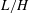 $L/H$ , the solution depends only on the shape of the velocity profiles in the feed streams and on the jet momentum-flux ratio. While conformal mapping can be used to determine the potential solution corresponding to uniform velocity profiles, numerical integration is required in general to compute rotational flows, including those arising with Poiseuille velocity profiles, with simplified solutions found in the limits
$L/H$ , the solution depends only on the shape of the velocity profiles in the feed streams and on the jet momentum-flux ratio. While conformal mapping can be used to determine the potential solution corresponding to uniform velocity profiles, numerical integration is required in general to compute rotational flows, including those arising with Poiseuille velocity profiles, with simplified solutions found in the limits 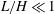 $L/H\ll 1$ and
$L/H\ll 1$ and 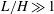 $L/H\gg 1$ . The results are used to quantify the near-stagnation-point region, of interest in counterflow-flame studies, including the local value of the strain rate as well as the curvature of the separating interface and the variations of the strain rate away from the stagnation point.
$L/H\gg 1$ . The results are used to quantify the near-stagnation-point region, of interest in counterflow-flame studies, including the local value of the strain rate as well as the curvature of the separating interface and the variations of the strain rate away from the stagnation point.
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 12
- Cited by


