Article contents
Aerothermodynamics of a sphere in a monatomic gas based on ab initio interatomic potentials over a wide range of gas rarefaction: subsonic flows
Published online by Cambridge University Press: 03 December 2024
Abstract
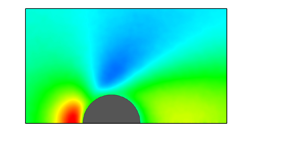
Aerothermodynamic characteristics of a sphere in a subsonic flow are calculated over a broad range of gas rarefaction by the direct simulation Monte Carlo method based on ab initio interatomic potentials and Cercignani–Lampis surface scattering kernel. Calculations of the drag and average energy transfer coefficients are performed for various noble gases in the range of Mach number from 0.1 to 1. The obtained results point out that the influence of the interatomic potential is weak in subsonic flows. A comparison of the present results with a linear theory shows that the numerical solutions at Mach number equal to 0.1 are close to those obtained from the linearized kinetic equation in the transitional and free-molecular regimes. In the near-continuum flow regime, the difference between the present solution and the linear theory is significant. To reveal the effects of the gas–surface accommodation, a few sets of the tangential momentum and normal energy accommodation coefficients are considered in simulations. It is shown that the effect of the accommodation coefficients on the sphere drag is not trivial, and, for non-diffuse scattering, the drag coefficient can be either larger or smaller than that for diffuse scattering. The effect of the sphere temperature is also investigated and the calculated values of the average energy transfer coefficient are used to find the Stanton number, recovery factor and adiabatic surface temperature. The numerical results for the sphere drag and energy transfer are compared with the semi-empirical fitting equations known from the literature.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 1
- Cited by


