Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T07:06:43.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplitude and frequency modulation in wall turbulence

Published online by Cambridge University Press:  27 September 2012

B. Ganapathisubramani ,
N. Hutchins ,
J. P. Monty ,
D. Chung  and
I. Marusic
B. Ganapathisubramani*
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
N. Hutchins
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
J. P. Monty
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
D. Chung
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
I. Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Melbourne, VIC 3010, Australia
*
†Email address for correspondence: G.Bharath@soton.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study we examine the impact of the strength of the large-scale motions on the amplitude and frequency of the small scales in high-Reynolds-number turbulent boundary layers. Time series of hot-wire data are decomposed into large- and small-scale components, and the impact of the large scale on the amplitude and frequency of the small scales is considered. The amplitude modulation effect is examined by conditionally averaging the small-scale intensity (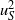${ u}_{S}^{2} $) for various values of the large-scale fluctuation (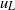${u}_{L} $). It is shown that 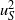${ u}_{S}^{2} $ increases with increasing value of 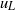${u}_{L} $ in the near-wall region, whereas, farther away from the wall, 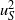${ u}_{S}^{2} $ decreases with increasing 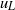${u}_{L} $. The rate of increase in small-scale intensity with the strength of the large-scale signal is neither symmetric (about 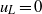${u}_{L} = 0$) nor linear. The extent of the frequency modulation is examined by counting the number of occurrences of local maxima or minima in the small-scale signal. It is shown that the frequency modulation effect is confined to the near-wall region and its extent diminishes rapidly beyond 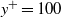${y}^{+ } = 100$. A phase lag between the large- and small-scale fluctuations, in terms of amplitude modulation, has also been identified, which is in agreement with previous studies. The phase lag between large- and small-scale fluctuations for frequency modulation is comparable to that of amplitude modulation in the near-wall region. The combined effect of both amplitude and frequency modulation is also examined by computing conditional spectra of the small-scale signal conditioned on the large scales. In the near-wall region, the results indicate that the peak value of pre-multiplied spectra increases with increasing value of 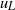${u}_{L} $, indicating amplitude modulation, while the frequency at which this peak occurs also increases with increasing value of 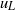${u}_{L} $, revealing frequency modulation. The overall trends observed from the conditional spectra are consistent with the results obtained through statistical analyses. Finally, a physical mechanism that can capture most of the above observations is also presented.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 712 , 10 December 2012 , pp. 61 - 91
Copyright
©2012 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–53.Google Scholar
Bailey, S. C. C., Hultmark, M., Smits, A. & Schultz, M. P. 2008 Azimuthal structure of turbulence in high Reynolds number pipe flow. J. Fluid Mech. 615, 121–138.CrossRefGoogle Scholar
Bandyopadhyay, P. R. & Hussain, A. K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27 (9), 2221–2228.Google Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23 (6), 061701.Google Scholar
Blackwelder, R. F. & Kovasznay, L. S. G. 1972 Time scales and correlations in a turbulent boundary layer. Phys. Fluids 15, 1545–1554.Google Scholar
Brown, G. R. & Thomas, A. S. W. 1977 Large structure in a turbulent boundary layer. Phys. Fluids 20, S243–S251.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.CrossRefGoogle Scholar
Clauser, F. H. 1956 The turbulent boundary layer. Adv. Mech. 4, 1–51.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
Del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2008 On the limitations of Taylor’s hypothesis in constructing long structures in a turbulent boundary layer. J. Fluid Mech. 614, 197–206.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Guala, M., Hommema, S. E. & Adrian, R. J. 2006 Large-scale and very-large-scale motions in turbulent pipe flow. J. Fluid Mech. 554, 521–542.CrossRefGoogle Scholar
Guala, M., Metzger, M. & McKeon, B. J. 2011 Interactions within the turbulent boundary layer at high Reynolds number. J. Fluid Mech. 666, 573–604.Google Scholar
Hunt, J. C. R. & Morrison, J. F. 2000 Eddy structure in turbulent boundary layers. Eur. J. Mech (B/Fluids) 19, 673–694.Google Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering structures in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. 365, 647–664.Google Scholar
Hutchins, N., Monty, J. P., Ganapathisubramani, B., Ng, H. & Marusic, I. 2011 Three-dimensional conditional structure of a high Reynolds number turbulent boundary layer. J. Fluid Mech. 673, 255–285.Google Scholar
Hutchins, N., Nickels, T. B., Marusic, I. & Chong, M. S. 2009 Hot-wire spatial resolution issues in wall-bounded turbulence. J. Fluid Mech. 632, 431–442.Google Scholar
Kailashnath, K. & Sreenivasan, K. R. 1993 Zero crossings of velocity fluctuations in turbulent boundary layers. Phys. Fluids 5 (11), 2879–2885.Google Scholar
Kim, K. C. & Adrian, R. J. 1999 Very large-scale motion in the outer layer. Phys. Fluids 11 (2), 417–422.Google Scholar
Kovasznay, L. S. G., Kibens, V. & Blackwelder, R. F. 1970 Large-scale motion in the intermittent region of a turbulent boundary layer. J. Fluid Mech. 41, 283–326.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5, 407–417.CrossRefGoogle Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329 (5988), 193–196.CrossRefGoogle ScholarPubMed
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.Google Scholar
Meinhart, C. D. & Adrian, R. J. 1995 On the existence of uniform momentum zones in a turbulent boundary layer. Phys. Fluids 7 (4), 694–696.Google Scholar
Monty, J. P., Stewart, J. A., Williams, R. C. & Chong, M. S. 2007 Large-scale features in turbulent pipe and channel flows. J. Fluid Mech. 589, 147–156.Google Scholar
Nagib, H. & Chauhan, K. 2008 Variations of Von Kármán coefficient in canonical flows. Phys. Fluids 20, 101518.Google Scholar
Nickels, T. B., Marusic, I., Hafez, S. & Chong, M. S. 2005 Evidence of the ${k}^{\ensuremath{-} 1} $ law in high-Reynolds number turbulent boundary layer. Phys. Rev. Lett. 95, 074501.CrossRefGoogle Scholar
Nickels, T. B., Marusic, I., Hafez, S., Hutchins, N. & Chong, M. S. 2007 Some predictions of the attached eddy model for a high Reynolds number boundary layer. Phil. Trans. R. Soc. Lond. 265, 807–822.Google Scholar
Rao, K. N., Narasimha, R. & Narayanan, M. A. B. 1971 The phenomenon in a turbulent boundary layer. J. Fluid Mech. 48, 339–352.Google Scholar
Repetto, M. P. 2005 Cycle counting methods for bi-modal stationary Gaussian processes. Prob. Engng Mech. 20 (3), 229–238.Google Scholar
Rychlik, I. 1993 Characterisation of random fatigue loads. In Stochastic Approach to Fatigue (ed. Sobczyk, K), CISM Courses and Lectures , vol. 334. Springer.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22, 051704.Google Scholar
Sreenivasan, K. R. 1985 On the fine-scale intermittency of turbulence. J. Fluid Mech. 151, 81–103.CrossRefGoogle Scholar
Sreenivasan, K. R., Prabhu, A. & Narasimha, R. 1983 Zero-crossings in turbulent signals. J. Fluid Mech. 137, 251–272.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Wark, C. E. & Nagib, H. M. 1991 Experimental investigation of coherent structures in turbulent boundary layers. J. Fluid Mech. 230, 183–208.Google Scholar