Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-14T17:45:51.478Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplitude and frequency modulation of the small scales in a jet

Published online by Cambridge University Press:  08 May 2015

D. Fiscaletti ,
B. Ganapathisubramani  and
G. E. Elsinga
D. Fiscaletti*
Affiliation:
Laboratory for Aero and Hydrodynamics, Department of Mechanical, Maritime, and Materials Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628 CA, Delft, The Netherlands
B. Ganapathisubramani
Affiliation:
Aerodynamics and Flight Mechanics Research Group, University of Southampton, Southampton SO17 1BJ, UK
G. E. Elsinga
Affiliation:
Laboratory for Aero and Hydrodynamics, Department of Mechanical, Maritime, and Materials Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628 CA, Delft, The Netherlands
*
†Email address for correspondence: d.fiscaletti@tudelft.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

The present study is an experimental investigation of the relationship between the large- and small-scale motions in the far field of an air jet at high Reynolds number. In the first part of our investigation, the analysis is based on time series of hot-wire anemometry (HWA), which are converted into space series after applying the Taylor hypothesis. 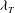By using a spectral filter, two signals are constructed, one representative of the large-scale motions ($2{\it\lambda}_{T}-L$, where ${\it\lambda}_{T}$ is the Taylor length scale, and 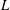$L$ is the integral length scale) and the other representative of the small-scale motions (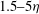$1.5{-}5{\it\eta}$, where 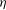${\it\eta}$ is the Kolmogorov length scale). The small-scale signal is found to be modulated both in amplitude and in frequency by the energy-containing scales in an analogous way, both at the centreline and around the centreline. In particular, for positive fluctuations of the large-scale signal, the small-scale signal is locally stronger in amplitude (amplitude modulation), and it locally exhibits a higher number of local maxima and minima (frequency modulation). The extent of this modulation is quantified based on the strength of the large-scale fluctuations. The response of the small-scale motions to amplitude modulation can be considered instantaneous, being on the order of one Kolmogorov time scale. In the second part of our investigation we use long-range 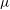${\it\mu}$PIV to study the behaviour of the small-scale motions in relation to their position in either high-speed or low-speed regions of the flow. The spatially resolved velocity vector fields allow us to quantify amplitude modulation directly in physical space. From this direct estimation in physical space, amplitude modulation is only 25 % of the value measured from HWA. The remaining 75 % comes from the fixed spectral band filter used to obtain the large- and small-scale signals, which does not consider the local convection velocity. A very similar overestimation of amplitude modulation when quantified in the time-frame is also obtained analytically. Furthermore, the size of the structures of intense vorticity does not change significantly in relation to the large-scale velocity fluctuation, meaning that there is no significant spatial frequency modulation. The remaining amplitude modulation in space can be explained as a statistical coupling between the strength of the structures of vorticity and their preferential location inside large-scale high-velocity regions. Finally, the implications that the present findings have on amplitude and frequency modulation in turbulent boundary layers (TBLs) are discussed.

JFM classification

Wakes/Jets: Jets Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 756 - 783
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.CrossRefGoogle Scholar
del Álamo, J. C. & Jiménez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.CrossRefGoogle Scholar
Ashurst, W. T., Kerstein, A. R., Kerr, R. M. & Gibson, C. H. 1987 Alignment of vorticity and scalar gradient with strain rate in simulated Navier–Stokes turbulence. Phys. Fluids 30, 2343–2353.CrossRefGoogle Scholar
Bandyopadhyay, P. R. & Hussain, K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27, 2221–2228.CrossRefGoogle Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: a refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.CrossRefGoogle Scholar
Buxton, O. R. H.2011 Fine scale features of turbulent shear flows. PhD thesis, Imperial College London.Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2014 Concurrent scale interactions in the far-field of a turbulent mixing layer. Phys. Fluids 26, 125106.CrossRefGoogle Scholar
Cardesa, J. I., Mistry, D., Gan, L. & Dawson, J. R. 2013 Invariants of the reduced velocity gradient tensor in turbulent flows. J. Fluid Mech. 716, 597–615.CrossRefGoogle Scholar
Chacin, J. M. & Cantwell, B. J. 2000 Dynamics of a low Reynolds number turbulent boundary layer. J. Fluid Mech. 404, 87–115.CrossRefGoogle Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.CrossRefGoogle Scholar
Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.CrossRefGoogle Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.CrossRefGoogle Scholar
Fiscaletti, D., Elsinga, G. E., Ganapathisubramani, B. & Westerweel, J.2013 Amplitude and frequency modulation of the small scales in a turbulent jet. In 8th International Symposium on Turbulence and Shear Flow Phenomena, 28–30 August, Poitiers.CrossRefGoogle Scholar
Fiscaletti, D., Westerweel, J. & Elsinga, G. E. 2014 Long-range ${\it\mu}$ PIV to resolve the small scales in a jet at high Reynolds number. Exp. Fluids 55, 1812.CrossRefGoogle Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 708, 1–31.Google Scholar
Ganapathisubramani, B., Lakshminarasimhan, K. & Clemens, N. T. 2008 Investigation of three-dimensional structure of fine scales in a turbulent jet by using cinematographic stereoscopic particle image velocimetry. J. Fluid Mech. 598, 141–175.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007a Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Hutchins, N. & Marusic, I. 2007b Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google ScholarPubMed
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence: DNS results. Flow Turbul. Combust. 91, 895–929.CrossRefGoogle Scholar
Ishihara, T., Toshiyuki, G. & Kaneda, Y. 2009 Study of high-Reynolds number isotropic turbulence by direct numerical simulation. Annu. Rev. Fluid Mech. 41, 165–180.CrossRefGoogle Scholar
Jacobi, I. & McKeon, B. J. 2013 Phase relationships between large and small scales in the turbulent boundary layer. Exp. Fluids 54, 1481.CrossRefGoogle Scholar
Jiménez, J. & Pinelli, A. 1999 The autonomous cycle of near-wall turbulence. J. Fluid Mech. 389, 335–359.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 225, 65–90.CrossRefGoogle Scholar
Kaneda, Y. & Ishihara, T. 2006 High-resolution direct numerical simulation of turbulence. J. Turbul. 7, 1–17.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.CrossRefGoogle ScholarPubMed
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Mathis, R., Marusic, I., Hutchins, N. & Sreenivasan, K. R. 2011 The relationship between the velocity skewness and the amplitude modulation of the small scale by the large scale in turbulent boundary layers. Phys. Fluids 23, 121702.CrossRefGoogle Scholar
Panchapakesan, N. R. & Lumley, J. L. 1993 Turbulence measurements in axisymmetric jets of air and helium. Part 1. Air jet. J. Fluid Mech. 246, 197–223.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Richardson, L. 1926 Atmospheric diffusion shown on a distance–neighbour graph. Proc. R. Soc. Lond. A 110, 709–737.Google Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: a note of caution. Phys. Fluids 22, 051704.CrossRefGoogle Scholar
Schoppa, W. & Hussain, F. 2002 Coherent structure generation in near-wall turbulence. J. Fluid Mech. 453, 57–108.CrossRefGoogle Scholar
She, Z. S., Jackson, E. & Orszag, S. A. 1990 Intermittent vortex structures in homogeneous isotropic turbulence. Nature 344, 226–228.CrossRefGoogle Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number ( $R_{{\it\lambda}}\sim 1000$ ) turbulent shear flow. Phys. Fluids 12, 2976–2989.CrossRefGoogle Scholar
Siggia, E. D. 1981 Numerical study of small-scale intermittency in three dimensional turbulence. J. Fluid Mech. 107, 375–406.CrossRefGoogle Scholar
Slot, H. J., Moore, P., Delfos, R. & Boersma, B. J. 2009 Experiments on the flow field and acoustic properties of a Mach number 0.75 turbulent air jet at a low Reynolds number. Flow Turbul. Combust. 83, 587–611.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Taylor, G. I. 1935 Statistical theory of turbulence: parts I–III. Proc. R. Soc. Lond. A 151, 421–464.CrossRefGoogle Scholar
Taylor, G. I. 1938 The spectrum of turbulence. Proc. R. Soc. Lond. A 164, 476–490.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1991 The spatial structure and statistical properties of homogeneous turbulence. J. Fluid Mech. 225, 1–20.CrossRefGoogle Scholar
Vincent, A. & Meneguzzi, M. 1994 The dynamics of vorticity tubes in homogeneous turbulence. J. Fluid Mech. 258, 245–254.CrossRefGoogle Scholar
Wei, L., Elsinga, G. E., Brethouwer, G., Schlatter, P. & Johansson, A. V. 2014 Universality and scaling phenomenology of small-scale turbulence in wall-bounded flows. Phys. Fluids 26, 035107.CrossRefGoogle Scholar
Worth, N. A. & Nickels, T. B. 2011 Some characteristics of thin shear layers in homogeneous turbulent flow. Phil. Trans. R. Soc. Lond. A 369, 709–722.Google ScholarPubMed
Zaman, K. B. M. Q. & Hussain, A. K. M. F. 1981 Taylor hypothesis and large-scale coherent structures. J. Fluid Mech. 112, 379–396.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar