Article contents
An active feedback flow control theory of the axisymmetric vortex breakdown process
Published online by Cambridge University Press: 15 June 2015
Abstract
An active feedback flow control theory of the axisymmetric vortex breakdown process in incompressible swirling flows in a finite-length straight circular pipe is developed. Flow injection distributed along the pipe wall is used as the controller. The flow is subjected to non-periodic inlet and outlet conditions where the inlet profiles of the axial velocity, circumferential velocity and azimuthal vorticity are prescribed, along with no radial velocity at the outlet. A long-wave asymptotic analysis at near-critical swirl ratios, which involves a rescaling of the axial distance and time, results in a model problem for the dynamics and the nonlinear control of both inviscid and high-Reynolds-number (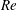 $\mathit{Re}$) flows. The approach provides the bifurcation diagram of steady states and the stability characteristics of these states. In addition, an energy analysis of the controlled flow dynamics suggests a feedback control law that relates the flow injection to the evolving maximum radial velocity at the inlet. Computed examples of the flow dynamics based on the full Euler and Navier–Stokes formulations at various swirl levels demonstrate the evolution to near-steady breakdown states when swirl is above a critical level that depends on
$\mathit{Re}$) flows. The approach provides the bifurcation diagram of steady states and the stability characteristics of these states. In addition, an energy analysis of the controlled flow dynamics suggests a feedback control law that relates the flow injection to the evolving maximum radial velocity at the inlet. Computed examples of the flow dynamics based on the full Euler and Navier–Stokes formulations at various swirl levels demonstrate the evolution to near-steady breakdown states when swirl is above a critical level that depends on 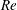 $\mathit{Re}$. Moreover, applying the proposed feedback control law during flow evolution shows for the first time the successful and robust elimination of the breakdown states and flow stabilization on an almost columnar state for a wide range of swirl (up to at least 30 %) above critical. The feedback control cuts the natural feed-forward mechanism of the breakdown process. Specifically, in the case of high-
$\mathit{Re}$. Moreover, applying the proposed feedback control law during flow evolution shows for the first time the successful and robust elimination of the breakdown states and flow stabilization on an almost columnar state for a wide range of swirl (up to at least 30 %) above critical. The feedback control cuts the natural feed-forward mechanism of the breakdown process. Specifically, in the case of high-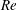 $\mathit{Re}$ flows, the control approach establishes a branch of columnar states for all swirl levels studied, where in the natural flow dynamics no such states exist. The present theory is limited to the control of axisymmetric flows in pipes where the wall boundary layer is thin and attached and does not interact with the flow in the bulk.
$\mathit{Re}$ flows, the control approach establishes a branch of columnar states for all swirl levels studied, where in the natural flow dynamics no such states exist. The present theory is limited to the control of axisymmetric flows in pipes where the wall boundary layer is thin and attached and does not interact with the flow in the bulk.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 10
- Cited by



