Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-28T07:49:28.167Z Has data issue: false hasContentIssue false
  • English
  • Français

An experimental investigation of the Rossby two-slit problem

Published online by Cambridge University Press:  17 April 2020

A. K. Kaminski Open the ORCID record for A. K. Kaminski [Opens in a new window] ,
K. R. Helfrich  and
J. Pedlosky
A. K. Kaminski*
Affiliation:
Applied Physics Laboratory, University of Washington, Seattle, WA98105, USA
K. R. Helfrich
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA02543, USA
J. Pedlosky
Affiliation:
Department of Physical Oceanography, Woods Hole Oceanographic Institution, Woods Hole, MA02543, USA
*
†Email address for correspondence: kaminska@uw.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

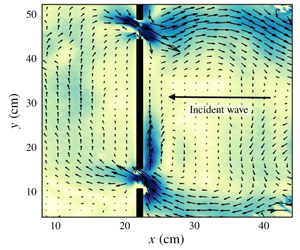
The problem of the transmission of wave energy through small gaps arises in a variety of physical contexts. Here we consider the problem of Rossby waves encountering a barrier with two small gaps. In contrast to waves encountering a barrier with one small gap, in which very little wave energy is predicted to transmit across the barrier, when there are two or more gaps linear theory predicts that the barrier may be surprisingly inefficient at blocking the transmission of Rossby wave energy, owing to the requirement that circulation be conserved around individual segments of the barrier. However, the theory neglects viscosity in the main basin interiors and nonlinear effects in the basins and the gaps. To examine these effects, here we present the results of a series of laboratory experiments in which Rossby basin modes interact with a barrier with zero, one or two gaps. We find that the large-scale waves are able to transmit across the barrier with two gaps as predicted by the theory. However, while the linear theory captures the large-scale flow structures, viscosity and nonlinearity significantly affect the flow along the boundaries and near the gaps in the barrier.

JFM classification

Geophysical and Geological Flows: Rotating flows Geophysical and Geological Flows: Waves in rotating fluids Geophysical and Geological Flows: Ocean processes
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 893 , 25 June 2020 , A4
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Godfrey, J. S. 1989 A Sverdrup model of the depth-integrated flow for the world ocean allowing for island circulations. Geophys. Astrophys. Fluid Dyn. 45, 89–112.CrossRefGoogle Scholar
Graef, F. & Magaard, L. 1994 Reflection of nonlinear baroclinic Rossby waves and the driving of secondary mean flows. J. Phys. Oceanogr. 24, 1867–1894.2.0.CO;2>CrossRefGoogle Scholar
van Heijst, G. J. F. 1994 Topography effects on vortices in a rotating fluid. Meccanica 19, 431–451.CrossRefGoogle Scholar
Johnson, E. R. & McDonald, N. R. 2005 Vortices near barriers with multiple gaps. J. Fluid Mech. 531, 335–358.CrossRefGoogle Scholar
Longuet-Higgins, M. S. 1964 Planetary waves on a rotating sphere. Proc. R. Soc. Lond. A 279, 446–473.Google Scholar
McKee, W. D. 1972 Scattering of Rossby waves by partial barriers. Geophys. Fluid Dyn. 4, 83–89.Google Scholar
Mercier, M. J., Garnier, N. B. & Dauxois, T. 2008 Reflection and diffraction of internal waves analyzed with the Hilbert transform. Phys. Fluids 20, 086601.CrossRefGoogle Scholar
Mysak, L. A. & Magaard, L. 1983 Rossby wave driven Eulerian mean flows along non-zonal barriers, with application to the Hawaiian Ridge. J. Phys. Oceanogr. 13, 1716–1725.2.0.CO;2>CrossRefGoogle Scholar
Pedlosky, J. 1965 A study of the time dependent ocean circulation. J. Atmos. Sci. 22, 267–272.2.0.CO;2>CrossRefGoogle Scholar
Pedlosky, J. 1967 Fluctuating winds and the ocean circulation. Tellus 19, 250–257.CrossRefGoogle Scholar
Pedlosky, J. 2000a The transmission and transformation of baroclinic Rossby waves by topography. J. Phys. Oceanogr. 30, 3077–3101.2.0.CO;2>CrossRefGoogle Scholar
Pedlosky, J. 2000b The transmission of Rossby waves through basin barriers. J. Phys. Oceanogr. 30, 495–511.2.0.CO;2>CrossRefGoogle Scholar
Pedlosky, J. 2001 The transparency of ocean barriers to Rossby waves: the Rossby slit problem. J. Phys. Oceanogr. 31, 336–352.2.0.CO;2>CrossRefGoogle Scholar
Pedlosky, J. & Greenspan, H. P. 1967 A simple laboratory model for the oceanic circulation. J. Fluid Mech. 27 (2), 291–304.CrossRefGoogle Scholar
Pedlosky, J., Pratt, L. J., Spall, M. A. & Helfrich, K. R. 1997 Circulation around islands and ridges. J. Mar. Res. 55, 1199–1251.CrossRefGoogle Scholar
Pedlosky, J. & Spall, M. A. 1999 Rossby normal modes in basins with barriers. J. Phys. Oceanogr. 29, 2332–2349.2.0.CO;2>CrossRefGoogle Scholar
Porter, D. 1972 The transmission of surface waves through a gap in a vertical barrier. Proc. Camb. Phil. Soc. 71, 411–421.CrossRefGoogle Scholar
Lord Rayleigh, 1897 On the passage of waves through apertures in plane screens, and allied problems. Phil. Mag. 43, 259–272.CrossRefGoogle Scholar
Spall, M. A. & Pedlosky, J. 2005 Reflection and transmission of equatorial Rossby waves. J. Phys. Oceanogr. 35, 363–373.CrossRefGoogle Scholar
Warren, B. A., Whitworth, T. III & LaCasce, J. H. 2002 Forced resonant undulation in the deep Mascarene Basin. Deep-Sea Res. II 49, 1513–1526.Google Scholar
Williams, P. D., Read, P. R. & Haine, T. W. N. 2010 Testing the limits of quasi-geostrophic theory: application to observed laboratory flows outside the quasi-geostrophic regime. J. Fluid Mech. 649, 187–203.CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G. J. F. 2002 Ekman effects in a rotating flow over bottom topography. J. Fluid Mech. 471, 239–255.CrossRefGoogle Scholar