Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Yin, Peiran
Li, Rui
Wang, Zizhe
Lin, Shaochun
Tian, Tian
Zhang, Liang
Wu, Longhao
Zhao, Jie
Duan, Changkui
Huang, Pu
and
Du, Jiangfeng
2019.
Manipulation of a Micro-Object Using Topological Hydrodynamic Tweezers.
Physical Review Applied,
Vol. 12,
Issue. 4,
Candelier, Fabien
Mehlig, Bernhard
and
Magnaudet, Jacques
2019.
Time-dependent lift and drag on a rigid body in a viscous steady linear flow.
Journal of Fluid Mechanics,
Vol. 864,
Issue. ,
p.
554.
Ku, Xiaoke
Li, Heng
Lin, Jianzhong
and
Jin, Hanhui
2019.
Accumulation of heavy particles in circular bounded vortex flows induced by two small rotating cylinders.
International Journal of Multiphase Flow,
Vol. 113,
Issue. ,
p.
71.
Krishnamurthy, Deepak
Li, Hongquan
Benoit du Rey, François
Cambournac, Pierre
Larson, Adam G.
Li, Ethan
and
Prakash, Manu
2020.
Scale-free vertical tracking microscopy.
Nature Methods,
Vol. 17,
Issue. 10,
p.
1040.
Rodgar, Majid
Scolan, Hélène
Marié, Jean-Louis
Doppler, Delphine
and
Matas, Jean-Philippe
2021.
Bubble behaviour in a horizontal high-speed solid-body rotating flow.
Journal of Fluid Mechanics,
Vol. 925,
Issue. ,
Romanò, Francesco
des Boscs, Pierre-Emmanuel
and
Kuhlmann, Hendrik C.
2021.
Stokesian motion of a spherical particle near a right corner made by tangentially moving walls.
Journal of Fluid Mechanics,
Vol. 927,
Issue. ,
Romanò, Francesco
2022.
Reconstructing the neutrally-buoyant particle flow near a singular corner.
Acta Mechanica Sinica,
Vol. 38,
Issue. 8,
Shen, Feng
Ai, Mingzhu
Li, Zonghe
Xue, Sen
Xu, Min
and
Liu, Zhaomiao
2022.
Particle orbiting motion and deviations from streamlines in a microvortex.
Applied Physics Letters,
Vol. 120,
Issue. 2,
Sahu, Toshan Lal
Paul, Immanuvel
and
Yu, Simon C. M.
2025.
Dynamics and predictive modeling of vertically rising bubble motion in rotating shear-thinning fluids.
Physics of Fluids,
Vol. 37,
Issue. 8,
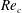 $Re_{c}$ . The radius of the observed orbits increases with Reynolds number more slowly than a typical Hopf bifurcation, in this case, growing as
$Re_{c}$ . The radius of the observed orbits increases with Reynolds number more slowly than a typical Hopf bifurcation, in this case, growing as 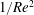 $1/Re^{2}$ .
$1/Re^{2}$ .

