Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T13:54:15.743Z Has data issue: false hasContentIssue false
  • English
  • Français

Analogies and differences between the stability of an isolated pancake vortex and a columnar vortex in stratified fluid

Published online by Cambridge University Press:  11 May 2016

Eunok Yim  and
Paul Billant
Eunok Yim*
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
Paul Billant
Affiliation:
LadHyX, CNRS, École Polytechnique, F-91128 Palaiseau CEDEX, France
*
†Email address for correspondence: eunok@ladhyx.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In order to understand the dynamics of pancake shaped vortices in stably stratified fluids, we perform a linear stability analysis of an axisymmetric vortex with Gaussian angular velocity in both the radial and axial directions with an aspect ratio of ${\it\alpha}$. The results are compared to those for a columnar vortex (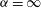${\it\alpha}=\infty$) in order to identify the instabilities. Centrifugal instability occurs when 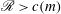$\mathscr{R}>c(m)$ where 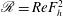$\mathscr{R}=ReF_{h}^{2}$ is the buoyancy Reynolds number, 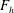$F_{h}$ the Froude number, 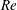$Re$ the Reynolds number and 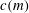$c(m)$ a constant which differs for the three unstable azimuthal wavenumbers 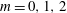$m=0,1,2$. The maximum growth rate depends mostly on 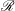$\mathscr{R}$ and is almost independent of the aspect ratio ${\it\alpha}$. For sufficiently large buoyancy Reynolds number, the axisymmetric mode is the most unstable centrifugal mode whereas for moderate 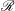$\mathscr{R}$, the mode 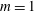$m=1$ is the most unstable. Shear instability for 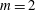$m=2$ develops only when 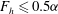$F_{h}\leqslant 0.5{\it\alpha}$. By considering the characteristics of shear instability for a columnar vortex with the same parameters, this condition is shown to be such that the vortex is taller than the minimum wavelength of shear instability in the columnar case. For larger Froude number 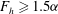$F_{h}\geqslant 1.5{\it\alpha}$, the isopycnals overturn and gravitational instability can operate. Just below this threshold, the azimuthal wavenumbers 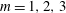$m=1,2,3$ are unstable to baroclinic instability. A simple model shows that baroclinic instability develops only above a critical vertical Froude number 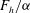$F_{h}/{\it\alpha}$ because of confinement effects.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Stratified flows Vortex Flows: Vortex instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 796 , 10 June 2016 , pp. 732 - 766
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A. & Brancher, P. 2004 Transient energy growth for the Lamb–Oseen vortex. Phys. Fluids 16, L1–L4.Google Scholar
Armi, L., Hebert, D., Oakey, N., Price, J. F., Richardson, P. L., Rossby, H. T. & Ruddick, B. 1989 Two years in the life of a mediterranean salt lens. J. Phys. Oceanogr. 19, 354–370.2.0.CO;2>CrossRefGoogle Scholar
Ash, R. L. & Khorrami, M. R. 1995 Fluid Vortices (ed. Green, S. I.), Fluid Mechanics and Its Applications, vol. 30, pp. 317–372. Springer.CrossRefGoogle Scholar
Balay, S., Abhyankar, S., Adams, M. F., Brown, J., Brune, P., Buschelman, K., Eijkhout, V., Gropp, W. D., Kaushik, D., Knepley, M. G. et al. 2014 PETSc users manual. Tech. Rep. ANL-95/11 – Revision 3.5. Argonne National Laboratory.CrossRefGoogle Scholar
Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14, 529–551.Google Scholar
Beckers, M., Clercx, H. J. H., van Heijst, G. J. F. & Verzicco, R. 2003 Evolution and instability of monopolar vortices in a stratified fluid. Phys. Fluids 15 (4), 1033–1045.CrossRefGoogle Scholar
Beckers, M., Verzicco, R., Clercx, H. J. H. & van Heijst, G. J. F. 2001 Dynamics of pancake-like vortices in a stratified fluid: experiments, model and numerical simulations. J. Fluid Mech. 433, 1–27.CrossRefGoogle Scholar
Billant, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 1. General stability equations. J. Fluid Mech. 660, 354–395.Google Scholar
Billant, P. & Chomaz, J.-M. 2000 Experimental evidence for a new instability of a vertical columnar vortex pair in a strongly stratified fluid. J. Fluid Mech. 418, 167–188.Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similary of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.Google Scholar
Billant, P., Deloncle, A., Chomaz, J.-M. & Otheguy, P. 2010 Zigzag instability of vortex pairs in stratified and rotating fluids. Part 2. Analytical and numerical analyses. J. Fluid Mech. 660, 396–429.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalized Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.Google Scholar
Billant, P. & Le Dizès, S. 2009 Waves on a columnar vortex in a strongly stratified fluid. Phys. Fluids 21, 106602.Google Scholar
Bonnier, M., Eiff, O. & Bonneton, P. 2000 On the density structure of far-wake vortices in a stratified fluid. Dyn. Atmos. Oceans 31 (14), 117–137.Google Scholar
Carton, X. & Legras, B. 1994 The life-cycle of tripoles in two-dimensional incompressible flows. J. Fluid Mech. 267, 53–82.Google Scholar
Chomaz, J.-M., Bonneton, P., Butet, A. & Hopfinger, E. J. 1993 Vertical diffusion of the far wake of a sphere moving in a stratified fluid. Phys. Fluids 5 (11), 2799–2806.Google Scholar
De Vuyst, F.2013 Numerical modeling of transport problems using freefem $++$ software – with examples in biology, CFD, traffic flow and energy transfer. Lecture, ENS Cachan. Available at: https://cel.archives-ouvertes.fr/cel-00842234.Google Scholar
Deloncle, A., Billant, P. & Chomaz, J.-M. 2011 Three-dimensional stability of vortex arrays in a stratified and rotating fluid. J. Fluid Mech. 678, 482–510.Google Scholar
Deloncle, A., Chomaz, J.-M. & Billant, P. 2007 Three-dimensional stability of a horizontally sheared flow in a stably stratified fluid. J. Fluid Mech. 570, 297–305.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Eady, E. T. 1949 Long waves and cyclone waves. Tellus 1 (3), 33–52.Google Scholar
Eliassen, A. 1983 The charney–stern theorem on barotropic-baroclinic instability. Pure Appl. Geophys. 121 (3), 563–572.Google Scholar
Eliassen, A. & Kleinschmidt, E. Jr. 1957 Dynamic meteorology. In Geophysik II/Geophysics II (ed. Bartels, J.), Handbuch der Physik/Encyclopedia of Physics, vol. 0/48, pp. 1–154. Springer.Google Scholar
Elman, H. C., Silvester, D. J. & Wathen, A. J. 2005 Finite Elements and Fast Iterative Solvers: with Applications in Incompressible Fluid Dynamics: with Applications in Incompressible Fluid Dynamics. Oxford University Press.Google Scholar
Fabre, D. & Jacquin, L. 2004 Viscous instabilities in trailing vortices at large swirl numbers. J. Fluid Mech. 500, 239–262.CrossRefGoogle Scholar
Fincham, A. M., Maxworthy, T. & Spedding, G. R. 1996 Energy dissipation and vortex structure in freely decaying, stratified grid turbulence. Dyn. Atmos. Oceans 23 (14), 155–169.Google Scholar
Flór, J. B. & van Heijst, G. J. F. 1996 Stable and unstable monopolar vortices in a stratified fluid. J. Fluid Mech. 311, 257–287.Google Scholar
Garnaud, X.2012 Modes, transient dynamics and forced response of circular jets. PhD thesis, LadHyX, Ecole Polytechnique X.Google Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.Google Scholar
Gent, P. R. & McWilliams, J. C. 1986 The instability of barotropic circular vortices. Geophys. Astrophys. Fluid Dyn. 35 (1–4), 209–233.Google Scholar
Godoy-Diana, R. & Chomaz, J.-M. 2003 Effect of the schmidt number on the diffusion of axisymmetric pancake vortices in a stratified fluid. Phys. Fluids 15 (4), 1058–1064.Google Scholar
Hecht, F. 2012 New development in freefem + +. J. Numer. Math. 20 (3–4), 251–265.CrossRefGoogle Scholar
Hernandez, V., Roman, J. E. & Vidal, V. 2005 SLEPc: a scalable and flexible toolkit for the solution of eigenvalue problems. ACM Trans. Math. Softw. 31 (3), 351–362.Google Scholar
Hobbs, R. 2007 Go (geophysical oceanography): a new tool to understand the thermal structure and dynamics of oceans. Eur. Union News. 2, 7.Google Scholar
Hoskins, B. J., McIntyre, M. E. & Robertson, A. W. 1985 On the use and significance of isentropic potential vorticity maps. Q. J. R. Meteorol. Soc. 111 (470), 877–946.Google Scholar
Lazar, A., Stegner, A. & Heifetz, E. 2013 Inertial instability of intense stratified anticyclones. Part 1. Generalized stability criterion. J. Fluid Mech. 732, 457–484.Google Scholar
Le Dizès, S. & Billant, P. 2009 Radiative instability in stratified vortices. Phys. Fluids 21, 096602.Google Scholar
Lin, Q., Boyer, D. L. & Fernando, H. J. S. 1992 Turbulent wakes of linearly stratified flow past a sphere. Phys. Fluids A 4 (48), 1687–1696.Google Scholar
McIntyre, M. E. 1970 Diffusive destabilization of the baroclinic circular vortex. Geophys. Fluid Dyn. 1, 19–57.Google Scholar
Ménesguen, C., Hua, B. L., Carton, X., Klingelhoefer, F., Schnrle, P. & Reichert, C. 2012 Arms winding around a meddy seen in seismic reflection data close to the Morocco coastline. Geophys. Res. Lett. 39 (5), L05604.Google Scholar
Meunier, P., Miquel, B. & Le Dizès, S. 2014 Instabilities around a rotating ellipsoid in a stratified rotating flow. In 19th Australasian Fluid Mechanics Conference, Melbourne, Australia (ed. Chowdhury, H. & Alam, F.). RMIT University.Google Scholar
Negretti, M. E. & Billant, P. 2013 Stability of a Gaussian pancake vortex in a stratified fluid. J. Fluid Mech. 718, 457–480.CrossRefGoogle Scholar
Otheguy, P., Chomaz, J.-M. & Billant, P. 2006 Elliptic and zigzag instabilities on co-rotating vertical vortices in a stratified fluid. J. Fluid Mech. 553, 253–272.CrossRefGoogle Scholar
Plougonven, R. & Zeitlin, V. 2002 Internal gravity wave emission from a pancake vortex: An example of wave-vortex interaction in strongly stratified flows. Phys. Fluids 14 (3), 1259–1268.Google Scholar
Rayleigh, L. 1880 On the stability, or instability, of certain fluid motions. Proc. Lond. Math. Soc. 11, 57–70.Google Scholar
Richardson, P. L., Bower, A. S. & Zenk, W. 2000 A census of meddies tracked by floats. Prog. Oceanogr. 45, 209–250.Google Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2010 Viscous stability properties of a Lamb–Oseen vortex in a stratified fluid. J. Fluid Mech. 645, 255–278.CrossRefGoogle Scholar
Smyth, W. D. & Mcwilliams, J. C. 1998 Instability of an axisymmetric vortex in a stably stratified, rotating environment. Theor. Comput. Fluid Dyn. 11 (3–4), 305–322.CrossRefGoogle Scholar
Solberg, H. 1936 Le mouvement d’inertie de l’atmosphère stable et son rôle dans la théorie des cyclones. Meteor. Assoc. U.G.G.I.. pp. 66–82. Dupont.Google Scholar
Spedding, G. R., Browand, F. K. & Fincham, A. M. 1996 Turbulence, similarity scaling and vortex geometry in the wake of a towed sphere in a stably stratified fluid. J. Fluid Mech. 314, 53–103.Google Scholar
Vallis, G. K. 2006 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-scale Circulation. Cambridge University Press.CrossRefGoogle Scholar
Yim, E. & Billant, P. 2015 On the mechanism of the gent-mcwilliams instability of a columnar vortex in stratified rotating fluids. J. Fluid Mech. 780, 5–44.Google Scholar