Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T01:52:12.813Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of passive flexion in propelling a plunging plate using a torsion spring model

Published online by Cambridge University Press:  25 October 2018

N. Arora ,
C.-K. Kang Open the ORCID record for C.-K. Kang [Opens in a new window] ,
W. Shyy  and
A. Gupta Open the ORCID record for A. Gupta [Opens in a new window]
N. Arora
Affiliation:
Faculty of Mechanical Engineering, Technion – Israel Institute of Technology, Haifa, 3200003, Israel
C.-K. Kang
Affiliation:
Department of Mechanical and Aerospace Engineering, University of Alabama in Huntsville, Huntsville, AL 35899, USA
W. Shyy
Affiliation:
Department of Mechanical and Aerospace Engineering, Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong
A. Gupta*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology, Hauz Khas, New Delhi, 110016, India
*
†Email address for correspondence: agupta@mech.iitd.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We mimic a flapping wing through a fluid–structure interaction (FSI) framework based upon a generalized lumped-torsional flexibility model. The developed fluid and structural solvers together determine the aerodynamic forces, wing deformation and self-propelled motion. A phenomenological solution to the linear single-spring structural dynamics equation is established to help offer insight and validate the computations under the limit of small deformation. The cruising velocity and power requirements are evaluated by varying the flapping Reynolds number (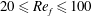$20\leqslant Re_{f}\leqslant 100$), stiffness (represented by frequency ratio, 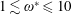$1\lesssim \unicode[STIX]{x1D714}^{\ast }\leqslant 10$) and the ratio of aerodynamic to structural inertia forces (represented by a dimensionless parameter 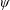$\unicode[STIX]{x1D713}$ (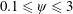$0.1\leqslant \unicode[STIX]{x1D713}\leqslant 3$)). For structural inertia dominated flows (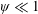$\unicode[STIX]{x1D713}\ll 1$), pitching and plunging are shown to always remain in phase (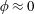$\unicode[STIX]{x1D719}\approx 0$) with the maximum wing deformation occurring at the end of the stroke. When aerodynamics dominates (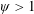$\unicode[STIX]{x1D713}>1$), a large phase difference is induced (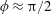$\unicode[STIX]{x1D719}\approx \unicode[STIX]{x03C0}/2$) and the maximum deformation occurs at mid-stroke. Lattice Boltzmann simulations show that there is an optimal 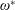$\unicode[STIX]{x1D714}^{\ast }$ at which cruising velocity is maximized and the location of optimum shifts away from unit frequency ratio (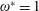$\unicode[STIX]{x1D714}^{\ast }=1$) as $\unicode[STIX]{x1D713}$ increases. Furthermore, aerodynamics administered deformations exhibit better performance than those governed by structural inertia, quantified in terms of distance travelled per unit work input. Closer examination reveals that although maximum thrust transpires at unit frequency ratio, it is not transformed into the highest cruising velocity. Rather, the maximum velocity occurs at the condition when the relative tip displacement 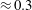${\approx}\,0.3$.

JFM classification

Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 562 - 604
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adkins, W. A. & Davidson, M. G. 2012 Ordinary Differential Equations. Springer.Google Scholar
Aidun, C. K., Lu, Y. & Ding, E. J. 1998 Direct analysis of particulate suspensions with inertia using the discrete Boltzmann equation. J. Fluid Mech. 373, 287–311.Google Scholar
Alben, S. 2008 Optimal flexibility of a flapping appendage in an inviscid fluid. J. Fluid Mech. 614, 355–380.Google Scholar
Alben, S. & Shelley, M. 2005 Coherent locomotion as an attracting state for a free flapping body. Proc. Natl Acad. Sci. USA 102 (32), 11163.Google Scholar
Alben, S., Witt, C., Baker, T. V., Anderson, E. & Lauder, G. V. 2012 Dynamics of freely swimming flexible foils. Phys. Fluids 24 (5), 051901.Google Scholar
Alexander, R. M. 2003 Principles of Animal Locomotion. Princeton University Press.Google Scholar
Alexander, D. E. 2004 Nature’s Flyers: Birds, Insects, and the Biomechanics of Flight. Johns Hopkins University Press.Google Scholar
Anderson, J. M., Streitlien, K., Barrett, D. S. & Triantafyllou, M. S. 1998 Oscillating foils of high propulsive efficiency. J. Fluid Mech. 360, 41–72.Google Scholar
Arora, N., Gupta, A., Sanghi, S., Aono, H. & Shyy, W. 2014 Lift-drag and flow structures associated with the clap and fling motion. Phys. Fluids 26 (7), 071906.Google Scholar
Arora, N., Gupta, A., Sanghi, S., Aono, H. & Shyy, W. 2016a Flow patterns and efficiency-power characteristics of a self-propelled, heaving rigid flat plate. J. Fluids Struct. 66, 517–542.Google Scholar
Arora, N., Gupta, A. & Shyy, W. 2016b A shifting discontinuous-grid-block lattice Boltzmann method for moving boundary simulations. Comput. Fluids 125, 59–70.Google Scholar
Azuma, A. & Watanabe, T. 1988 Flight performance of a dragonfly. J. Expl Biol. 137 (1), 221–252.Google Scholar
Beatus, T. & Cohen, I. 2015 Wing-pitch modulation in maneuvering fruit flies is explained by an interplay between aerodynamics and a torsional spring. Phys. Rev. E 92 (2), 022712.Google Scholar
Brennen, C. E.1982 A review of added mass and fluid inertial forces. Tech. Rep. Naval Civil Engineering Laboratory.Google Scholar
Brodsky, A. K. 1994 The Evolution of Insect Flight. Oxford University Press.Google Scholar
Chen, J. S., Chen, J. Y. & Chou, Y. F. 2008 On the natural frequencies and mode shapes of dragonfly wings. J. Sound Vib. 313 (3), 643–654.Google Scholar
Combes, S. A. & Daniel, T. L. 2003a Flexural stiffness in insect wings. Part I. Scaling and the influence of wing venation. J. Expl Biol. 206 (17), 2979–2987.Google Scholar
Combes, S. A. & Daniel, T. L. 2003b Flexural stiffness in insect wings. Part II. Spatial distribution and dynamic wing bending. J. Expl Biol. 206 (17), 2989–2997.Google Scholar
Dai, H., Luo, H. & Doyle, J. F. 2012 Dynamic pitching of an elastic rectangular wing in hovering motion. J. Fluid Mech. 693, 473–499.Google Scholar
Dickinson, M. H. & Gotz, K. G. 1993 Unsteady aerodynamic performance of model wings at low Reynolds numbers. J. Expl Biol. 174 (1), 45–64.Google Scholar
Dudley, R. 2002 The Biomechanics of Insect Flight: Form, Function, Evolution. Princeton University Press.Google Scholar
Eldredge, J. D., Toomey, J. & Medina, A. 2010 On the roles of chord-wise flexibility in a flapping wing with hovering kinematics. J. Fluid Mech. 659, 94–115.Google Scholar
Ellington, C. P. 1984a The aerodynamics of hovering insect flight. Part I. The quasi-steady analysis. Phil. Trans. R. Soc. Lond. B 305, 1–15.Google Scholar
Ellington, C. P. 1984b The aerodynamics of hovering insect flight. Part IV. Aeorodynamic mechanisms. Phil. Trans. R. Soc. Lond. B 305 (1122), 79–113.Google Scholar
Ellington, C. P., Van Den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.Google Scholar
Ennos, A. R. 1989 Inertial and aerodynamic torques on the wings of diptera in flight. J. Expl Biol. 142 (1), 87–95.Google Scholar
Evans, D. H. & Claiborne, J. B. 2005 The Physiology of Fishes, 3rd edn. Taylor & Francis.Google Scholar
Fuller, S. B., Karpelson, M., Censi, A., Ma, K. Y. & Wood, R. J. 2014 Controlling free flight of a robotic fly using an onboard vision sensor inspired by insect ocelli. J. R. Soc. Interface 11 (97), 20140281.Google Scholar
Genta, G. 2009 Vibration Dynamics and Control. Springer.Google Scholar
Heathcote, S. & Gursul, I. 2007 Flexible flapping airfoil propulsion at low Reynolds numbers. AIAA J. 45 (5), 1066–1079.Google Scholar
Heathcote, S., Martin, D. & Gursul, I. 2004 Flexible flapping airfoil propulsion at zero freestream velocity. AIAA J. 42 (11), 2196–2204.Google Scholar
Hua, R. N., Zhu, L. & Lu, X. Y. 2013 Locomotion of a flapping flexible plate. Phys. Fluids 25 (12), 121901.Google Scholar
Ishihara, D., Horie, T. & Denda, M. 2009 A two-dimensional computational study on the fluid–structure interaction cause of wing pitch changes in dipteran flapping flight. J. Expl Biol. 212 (1), 1–10.Google Scholar
Kang, C. K., Aono, H., Cesnik, C. E. S. & Shyy, W. 2011 Effects of flexibility on the aerodynamic performance of flapping wings. J. Fluid Mech. 689, 32–74.Google Scholar
Kang, C.-K., Cranford, J., Sridhar, M. K., Kodali, D., Landrum, D. B. & Slegers, N. 2017 Experimental characterization of a butterfly in climbing flight. AIAA J. 56, 15–24.Google Scholar
Kang, C. K. & Shyy, W. 2013 Scaling law and enhancement of lift generation of an insect-size hovering flexible wing. J. R. Soc. Interface 10 (85), 20130361.Google Scholar
Kang, C. K. & Shyy, W. 2014 Analytical model for instantaneous lift and shape deformation of an insect-scale flapping wing in hover. J. R. Soc. Interface 11 (101), 20140933.Google Scholar
Katz, J. & Weihs, D. 1978 Hydrodynamic propulsion by large amplitude oscillation of an airfoil with chordwise flexibility. J. Fluid Mech. 88 (3), 485–497.Google Scholar
Katz, J. & Weihs, D. 1979 Large amplitude unsteady motion of a flexible slender propulsor. J. Fluid Mech. 90 (4), 713–723.Google Scholar
Keennon, M., Klingebiel, K., Won, H. & Andriukov, A.2012 Development of the nano hummingbird: A tailless flapping wing micro air vehicle. In AIAA Aerospace Sciences Meeting, pp. 1–24. AIAA Reston.Google Scholar
Kodali, D. & Kang, C. K. 2016 An analytical model and scaling of chordwise flexible flapping wings in forward flight. Bioinspir. Biomim. 12 (1), 016006.Google Scholar
Korotkin, A. I. 2008 Added Masses of Ship Structures. Springer Science and Business Media.Google Scholar
Liu, Y., Cheng, B., Sane, S. P. & Deng, X. 2015 Aerodynamics of dynamic wing flexion in translating wings. Exp. Fluids 56 (6), 131.Google Scholar
Ma, K. Y., Chirarattananon, P. & Wood, R. J. 2015 Design and fabrication of an insect-scale flying robot for control autonomy. In International Conference on Intelligent Robots and Systems (IROS), 2015 IEEE/RSJ, pp. 1558–1564. IEEE.Google Scholar
Masoud, H. & Alexeev, A. 2010 Resonance of flexible flapping wings at low Reynolds number. Phys. Rev. E 81 (5), 056304.Google Scholar
Medina, C. & Kang, C.-K. 2018 An analytical solution to the aeroelastic response of a two-dimensional elastic plate in axial potential flow. J. Fluid Mech. 845, R3.Google Scholar
Moore, M. N. J. 2014 Analytical results on the role of flexibility in flapping propulsion. J. Fluid Mech. 757, 599–612.Google Scholar
Moore, M. N. J. 2015 Torsional spring is the optimal flexibility arrangement for thrust production of a flapping wing. Phys. Fluids 27 (9), 091701.Google Scholar
Olivier, M. & Dumas, G. 2016a Effects of mass and chordwise flexibility on 2D self-propelled flapping wings. J. Fluids Struct. 64, 46–66.Google Scholar
Olivier, M. & Dumas, G. 2016b A parametric investigation of the propulsion of 2D chordwise-flexible flapping wings at low Reynolds number using numerical simulations. J. Fluids Struct. 63, 210–237.Google Scholar
Paraz, F., Schouveiler, L. & Eloy, C. 2016 Thrust generation by a heaving flexible foil: resonance, nonlinearities, and optimality. Phys. Fluids 28 (1), 011903.Google Scholar
Prempraneerach, P., Hover, F. S. & Triantafyllou, M. S. 2003 The effect of chordwise flexibility on the thrust and efficiency of a flapping foil. In Proc. 13th Int. Symp. on Unmanned Untethered Submersible Technology: Special Session on Bioengineering Research Related to Autonomous Underwater Vehicles, New Hampshire, pp. 152–170. Autonomous Undersea Systems Institute.Google Scholar
Qi, D., Liu, Y., Shyy, W. & Aono, H. 2010 Simulations of dynamics of plunge and pitch of a three-dimensional flexible wing in a low Reynolds number flow. Phys. Fluids 22 (9), 091901.Google Scholar
Ramananarivo, S., Godoy-Diana, R. & Thiria, B. 2011 Rather than resonance, flapping wing flyers may play on aerodynamics to improve performance. Proc. Natl Acad. Sci. USA 108 (15), 5964–5969.Google Scholar
Sader, J. E. 1998 Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 84 (1), 64–76.Google Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206 (23), 4191–4208.Google Scholar
Shih, C. C. & Buchanan, H. J. 1971 The drag on oscillating flat plates in liquids at low Reynolds numbers. J. Fluid Mech. 48 (2), 229–239.Google Scholar
Shyy, W., Aono, H., Chimakurthi, S. K., Trizila, P., Kang, C. K., Cesnik, C. E. S. & Liu, H. 2010 Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 46 (7), 284–327.Google Scholar
Shyy, W., Aono, H., Kang, C.-K. & Liu, H. 2013 An Introduction to Flapping Wing Aerodynamics. Cambridge University Press.Google Scholar
Shyy, W., Kang, C.-K., Chirarattananon, P., Ravi, S. & Liu, H. 2016 Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. Lond. A 472 (2186), 20150712.Google Scholar
Spagnolie, S. E., Moret, L., Shelley, M. J. & Zhang, J. 2010 Surprising behaviors in flapping locomotion with passive pitching. Phys. Fluids 22 (4), 041903.Google Scholar
Tang, C., Huang, H., Gao, P. & Lu, X.-Y. 2016 Self-propulsion of a flapping flexible plate near the ground. Phys. Rev. E 94 (3), 033113.Google Scholar
Taylor, G., Triantafyllou, M. S. & Tropea, C. 2010 Animal Locomotion. Springer Science and Business Media.Google Scholar
Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. 2003 Flying and swimming animals cruise at a Strouhal number tuned for high power efficiency. Nature 425 (6959), 707–711.Google Scholar
Techet, A. H.2005 Hydrodynamics. Lecture notes available at http://ocw.mit.edu/courses/mechanical-engineering/2-016-hydrodynamic-13-012-fall-2005/readings/2005reading6.pdf.Google Scholar
Thiria, B. & Godoy-Diana, R. 2010 How wing compliance drives the efficiency of self-propelled flapping flyers. Phys. Rev. E 82 (1), 015303.Google Scholar
Thomson, W. 1996 Theory of Vibration with Applications. CRC Press.Google Scholar
Toomey, J. & Eldredge, J. D. 2008 Numerical and experimental study of the fluid dynamics of a flapping wing with low order flexibility. Phys. Fluids 20 (7), 073603.Google Scholar
Triantafyllou, M. S., Triantafyllou, G. S. & Yue, D. K. P. 2000 Hydrodynamics of fishlike swimming. Annu. Rev. Fluid Mech. 32 (1), 33–53.Google Scholar
Van Eysden, C. A. & Sader, J. E. 2007 Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope: arbitrary mode order. J. Appl. Phys. 101 (4), 044908.Google Scholar
Vandenberghe, N., Zhang, J. & Childress, S. 2004 Symmetry breaking leads to forward flapping flight. J. Fluid Mech. 506, 147–155.Google Scholar
Vanella, M., Fitzgerald, T., Preidikman, S., Balaras, E. & Balachandran, B. 2009 Influence of flexibility on the aerodynamic performance of a hovering wing. J. Expl Biol. 212 (1), 95–105.Google Scholar
Wu, P., Ifju, P. & Stanford, B. 2010 Flapping wing structural deformation and thrust correlation study with flexible membrane wings. AIAA J. 48 (9), 2111–2122.Google Scholar
Xiao, Q., Hu, J. & Liu, H. 2014 Effect of torsional stiffness and inertia on the dynamics of low aspect ratio flapping wings. Bioinspir. Biomim. 9 (1), 016008.Google Scholar
Yeh, P. D. & Alexeev, A. 2014 Free swimming of an elastic plate plunging at low Reynolds number. Phys. Fluids 26 (5), 053604.Google Scholar
Yeh, P. D. & Alexeev, A. 2016 Effect of aspect ratio in free-swimming plunging flexible plates. Comput. Fluids 124, 220–225.Google Scholar
Yin, B. & Luo, H. 2010 Effect of wing inertia on hovering performance of flexible flapping wings. Phys. Fluids 22 (11), 111902.Google Scholar
Zhang, J., Liu, N. S. & Lu, X. Y. 2010 Locomotion of a passively flapping flat plate. J. Fluid Mech. 659, 43–68.Google Scholar
Zhao, L., Deng, X. & Sane, S. P. 2011 Modulation of leading edge vorticity and aerodynamic forces in flexible flapping wings. Bioinspir. Biomim. 6 (3), 036007.Google Scholar
Zhao, L., Huang, Q., Deng, X. & Sane, S. P. 2010 Aerodynamic effects of flexibility in flapping wings. J. R. Soc. Interface 7 (44), 485–497.Google Scholar
Zhu, X., He, G. & Zhang, X. 2014a How flexibility affects the wake symmetry properties of a self-propelled plunging foil. J. Fluid Mech. 751, 164–183.Google Scholar
Zhu, X., He, G. & Zhang, X. 2014b Numerical study on hydrodynamic effect of flexibility in a self-propelled plunging foil. Comput. Fluids 97, 1–20.Google Scholar