Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T04:12:30.712Z Has data issue: false hasContentIssue false
  • English
  • Français

Analysis of the hypersonic cross-flow instability with experimental wavenumber distributions

Published online by Cambridge University Press:  28 November 2019

Harrison B. Yates Open the ORCID record for Harrison B. Yates [Opens in a new window] ,
Matthew W. Tufts Open the ORCID record for Matthew W. Tufts [Opens in a new window]  and
Thomas J. Juliano Open the ORCID record for Thomas J. Juliano [Opens in a new window]
Harrison B. Yates
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN46556-5684, USA
Matthew W. Tufts
Affiliation:
Air Force Research Laboratory, Aerospace Systems Directorate, Wright-Patterson Air Force Base, OH45433-7542, USA
Thomas J. Juliano*
Affiliation:
Department of Aerospace and Mechanical Engineering, University of Notre Dame, Notre Dame, IN46556-5684, USA
*
†Email address for correspondence: tjuliano@nd.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

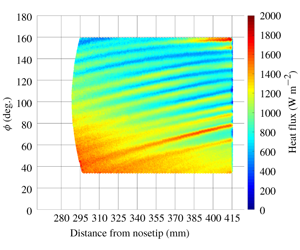
Stationary cross-flow vortex N-factors were calculated over the surface of a yawed circular cone using computationally predicted and experimentally observed wavenumber distributions. Surface heat-flux data were obtained on a $7^{\circ }$ half-angle circular cone to investigate the behaviour of the stationary waves at different angles of attack and Reynolds numbers at Mach 6 under quiet-flow conditions in the Boeing/AFOSR Mach-6 Quiet Tunnel at Purdue University. A wavelet analysis was conducted on the experimental surface heat-flux data to construct a spatial mapping of the local largest amplitude wavenumbers of the stationary cross-flow waves, which were between 40 and 80 per circumference. Significant axial and azimuthal variation was observed. The results from the wavelet analysis were used to inform the stability analysis. The computed integration marching directions demonstrated very good agreement with the experimentally observed paths. N-factors were first calculated by integrating the local amplification rate corresponding to the most amplified experimental wavenumbers. The calculations were repeated based on non-dimensional computationally varying wavenumber ratios, which were dimensionalized by the experimental data. The computed N-factors showed good agreement between the two techniques. N-factors were also computed using the computationally predicted most unstable wavenumbers. The results showed decreased agreement with the other two cases, suggesting that this assumption does not properly model the cross-flow transition process.

JFM classification

Aerodynamics: High-speed flow Boundary Layers: Boundary layer stability Compressible Flows: Compressible boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 883 , 25 January 2020 , A50
Copyright
© 2019 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, J. C. & Martindale, W. R.1973 Hypersonic lifting body windward surface flowfield analysis for high angles of incidence. Tech. Rep. 73-2. Arnold Engineering Development Center.CrossRefGoogle Scholar
Balakumar, P. & Owens, L. R.2009 Stability of supersonic boundary layers on a cone at an angle of attack. AIAA Paper 2009-3555.CrossRefGoogle Scholar
Balakumar, P. & Owens, L. R.2010 Stability of hypersonic boundary layers on a cone at an angle of attack. AIAA Paper 2010-4718.CrossRefGoogle Scholar
Boyd, C. F. & Howell, A.1994 Numerical Investigation of One-Dimensional Heat-Flux Calculations. Tech. Rep. NSWCDD/TR-94/114. Dahlgren Division Naval Surface Warfare Center.Google Scholar
Cerasuolo, S.2016 Heat flux measurements by infrared thermography in the Boeing/AFOSR Mach-6 Quiet Tunnel. Master’s thesis, University of Naples Federico II.Google Scholar
Chang, C.2003 The Langley stability and transition analysis code (LASTRAC): LST, linear & nonlinear PSE for 2-D, axisymmetric, and infinite swept wing boundary layers. AIAA Paper 2003-0974.Google Scholar
Chang, C.2004a The langley stability and transition analysis code (LASTRAC) version 1.2 user manual. NASA Tech. Rep. 2004-213233. Langley Research Center.Google Scholar
Chang, C.2004b LASTRAC.3d: transition prediction in 3D boundary layers. AIAA Paper 2004-2542.CrossRefGoogle Scholar
Chang, C.-L., Malik, M., Erlebacher, G. & Hussaini, M.1993 Linear and Nonlinear PSE for Compressible Boundary Layers. NASA Contractor Rep. 191537. ICASE Rep. No. 93-70. Institute for Computer Applications in Science and Engineering, NASA Langley Research Center.Google Scholar
Chynoweth, B. C.2015 A new roughness array for controlling the nonlinear breakdown of second-mode waves at Mach 6. Master’s thesis, Purdue University, West Lafayette, IN.Google Scholar
Daubechies, I. 1990 The wavelet transform time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 36 (5), 961–1004.CrossRefGoogle Scholar
Dinzl, D. J. & Candler, G. V. 2017 Direct simulation of hypersonic crossflow instability on an elliptic cone. AIAA J. 55 (6), 1769–1782.CrossRefGoogle Scholar
Edelman, J. B.2019 Nonlinear growth and breakdown of the hypersonic crossflow instability. PhD thesis, Purdue University, West Lafayette, IN.Google Scholar
Hirschen, C. & Gülhan, A. 2009 Infrared thermography and pitot pressure measurements of a scramjet nozzle flowfield. J. Propul. Power 25 (5), 1108–1120.CrossRefGoogle Scholar
InfraTec2016 Infrared-thermographic camera image IR. User Manual. InfraTec GmbH.Google Scholar
Juliano, T. J., Adamczak, D. & Kimmel, R. L.2014 HIFiRE-5 flight test heating analysis. AIAA Paper 2014-0076.CrossRefGoogle Scholar
Juliano, T. J., Paquin, L. A. & Borg, M. P. 2019 Measurement of HIFiRE-5 boundary-layer transition in a Mach-6 quiet tunnel with infrared thermography. AIAA J. 57 (5), 2001–2010.CrossRefGoogle Scholar
Juliano, T. J., Schneider, S. P. & Aradag, S. 2008 Quiet-flow Ludwieg tube for hypersonic transition research. AIAA J. 46 (7), 1757–1763.CrossRefGoogle Scholar
Kuehl, J. J.2016 Görtler modified mack-modes on a hypersonic flared cone. AIAA Paper 2016-0849.CrossRefGoogle Scholar
Kuehl, J. J., Perez, E. & Reed, H. L.2012 JoKHeR: NPSE simulations of hypersonic crossflow instability. AIAA Paper 2012-0921.CrossRefGoogle Scholar
Li, F., Choudhari, M., Chang, C. & White, J.2010 Analysis of instabilities in non-axisymmetric hypersonic boundary layers over cones. AIAA Paper 2010-4643.CrossRefGoogle Scholar
Lilly, J. M. & Olhede, S. C. 2012 Generalized Morse wavelets as a superfamily of analytic wavelets. IEEE Trans. Signal Process. 60 (11), 6036–6041.CrossRefGoogle Scholar
Malik, M. R. & Balakumar, P.1992 Instability and transition in three-dimensional supersonic boundary layers. AIAA Paper 1992-5049.CrossRefGoogle Scholar
Moyes, A. J., Kocian, T. S., Mullen, D. & Reed, H. L.2017 Boundary layer stability analysis of HIFiRE-5b flight geometry. AIAA Paper 2017-4301.CrossRefGoogle Scholar
Perez, E., Reed, H. L. & Kuehl, J. J.2013 Instabilities on a hypersonic yawed cone. AIAA Paper 2013-2879.CrossRefGoogle Scholar
Running, C. L., Sakaue, H. & Juliano, T. J. 2019 Stability and transition of three-dimensional boundary layers. Exp. Fluids 60, 23.CrossRefGoogle Scholar
Running, C. L., Thompson, M. J., Juliano, T. J. & Sakaue, H.2017 Boundary-layer separation detection for a cone at high angle of attack in Mach 4.5 flow with pressure-sensitive paint. AIAA Paper 2017-3120.CrossRefGoogle Scholar
Saric, W. S., Reed, H. L. & White, E. B. 2003 Stability and transition of three-dimensional boundary layers. Annu. Rev. Fluid Mech. 35 (1), 413–440.CrossRefGoogle Scholar
Schneider, S. P. 2008 Development of hypersonic quiet tunnels. J. Spacecr. Rockets 45 (4), 641–664.CrossRefGoogle Scholar
Schuele, C. Y.2011 Control of stationary crossflow modes using stationary patterned roughness and DBD plasma actuators at Mach 3.5. PhD thesis, University of Notre Dame, Notre Dame, IN.Google Scholar
Schuele, C. Y., Corke, T. & Matlis, E. 2013 Control of stationary crossflow modes in a Mach 3.5 boundary layer using patterned passive and active roughness. J. Fluid Mech. 718, 5–38.CrossRefGoogle Scholar
Torrence, C. & Compo, G. 1997 A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79 (1), 61–78.2.0.CO;2>CrossRefGoogle Scholar
van der Vegt, A. K. 1999 From Polymers to Plastics, 3rd edn. Delft Academic Press.Google Scholar
Ward, C. A. C.2014 Crossflow instability and transition on a circular cone at angle of attack in a Mach-6 quiet tunnel. PhD thesis, Purdue University, West Lafayette, IN.Google Scholar
Willems, S., Gülhan, A., Juliano, T. J., Kimmel, R. L. & Schneider, S. P.2014 Laminar to turbulent transition on the HIFiRE-1 cone at Mach 7 and high angle of attack. AIAA Paper 2014-0428.CrossRefGoogle Scholar
Yates, H. B., Juliano, T. J., Matlis, E. H. & Tufts, M. W.2018 Plasma-actuated flow control of hypersonic crossflow-induced boundary-layer transition in a Mach-6 quiet tunnel. AIAA Paper 2018-1076.CrossRefGoogle Scholar
Yates, H. B., Juliano, T. J., Matlis, E. H. & Tufts, M. W.2019 Crossflow transition acceleration with plasma actuators in hypersonic quiet flow. AIAA Paper 2019-1909.CrossRefGoogle Scholar